
【题目】某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)求出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
【答案】
(1)解:设y=kx+b,
把(22,36)与(24,32)代入得: ![]() ,
,
解得: ![]() ,
,
则y=﹣2x+80
(2)解:设当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是x元,
根据题意得:(x﹣20)y=150,
则(x﹣20)(﹣2x+80)=150,
整理得:x2﹣60x+875=0,
(x﹣25)(x﹣35)=0,
解得:x1=25,x2=35(不合题意舍去),
答:每本纪念册的销售单价是25元
(3)解:由题意可得:
w=(x﹣20)(﹣2x+80)
=﹣2x2+120x﹣1600
=﹣2(x﹣30)2+200,
此时当x=30时,w最大,
又∵售价不低于20元且不高于28元,
∴x<30时,y随x的增大而增大,即当x=28时,w最大=﹣2(28﹣30)2+200=192(元),
答:该纪念册销售单价定为28元时,才能使文具店销售该纪念册所获利润最大,最大利润是192元
【解析】1)抓住已知条件,y是x的一次函数,因此设y=kx+b,根据题意,利用待定系数法,建立方程组,解方程组求解,即可求出y与x的函数关系式。
(2)等量关系:(售价-进价)×销售量y=150,建立方程求解,再根据售价不低于20元且不高于28元,进而求出答案。
(3)根据w=(售价-进价)×销售量,列出函数关系式,将此函数解析式转化为顶点式,进而利用二次函数增减性及售价不低于20元且不高于28元求出答案。


科目:初中数学 来源: 题型:
【题目】下面说法正确的个数有( )
(1)二元一次方程组的两个方程的所有解,叫做二元一次方程组的解;
(2)如果![]() ,则
,则![]() ;
;
(3)三角形的外角等于与它不相邻的两个内角的和;
(4)多边形内角和等于![]() ;
;
(5)一组数据1,2,3,4,5的众数是0
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O在∠APB的平分线上,⊙O与PA相切于点C.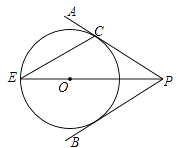
(1)求证:直线PB与⊙O相切;
(2)PO的延长线与⊙O交于点E.若⊙O的半径为3,PC=4.求弦CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD为正方形ABCD的对角线,BE平分∠DBC,交DC与点E,将△BCE绕点C顺时针旋转90°得到△DCF,若CE=1 cm,则BF=cm.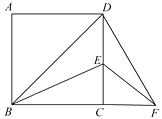
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“大美武汉,畅游江城”.某校数学兴趣小组就“最想去的武汉市旅游景点”随机调查了本校部分学生,要求每位同学选择且只能选择一个最想去的景点,下面是根据调查结果进行数据整理后绘制出的不完整的统计图:
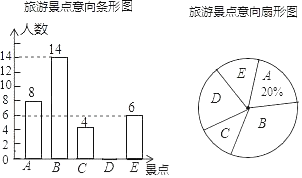
请根据图中提供的信息,解答下列问题:
(1)求被调查的学生总人数;
(2)补全条形统计图,并求扇形统计图中表示“最想去景点D”的扇形圆心角的度数;
(3)若该校共有1200名学生,请估计“最想去景点B“的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一批共享单车需要维修,维修后继续投放骑用,现有甲、乙两人做维修,甲每天维修16辆,乙每天维修的车辆比甲多8辆,甲单独维修完成这批共享单车比乙单独维修完多用20天,公司每天付甲80元维修费,付乙120元维修费.
(1)问需要维修的这批共享单车共有多少辆?
(2)在维修过程中,公司要派一名人员进行质量监督,公司负担他每天10元补助费,现有三种维修方案:①由甲单独维修;
②由乙单独维修;
③甲、乙合作同时维修,你认为哪种方案最省钱,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为原点,一次函数y1=x+m与反比例函数y2= ![]() 的图象相交于A(2,1),B(n,﹣2)两点,与x轴交于点C.
的图象相交于A(2,1),B(n,﹣2)两点,与x轴交于点C.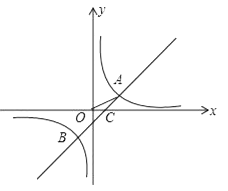
(1)求反比例函数解析式和点B坐标;
(2)当x的取值范围是时,有y1>y2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
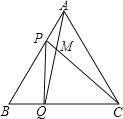
【题目】点P、Q分别是边长为4cm的等边![]() 的边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都是
的边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都是![]() ,设运动时间为t秒.
,设运动时间为t秒.
![]() 连接AQ、CP交于点M,则在P、Q运动的过程中,
连接AQ、CP交于点M,则在P、Q运动的过程中,![]() 变化吗:若变化,则说明理由,若不变,则求出它的度数;
变化吗:若变化,则说明理由,若不变,则求出它的度数;
![]() 连接PQ,
连接PQ,
![]() 当
当![]() 秒时,判断
秒时,判断![]() 的形状,并说明理由;
的形状,并说明理由;
![]() 当
当![]() 时,则
时,则![]() ______秒
______秒![]() 直接写出结果
直接写出结果![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com