
【题目】如图,在△ABC中,AB=AC,∠BAC=50°,∠BAC的角平分线AF与AB的垂直平分线DF交于点F,连接CF,BF,则∠BCF的度数为( )

A. 30°B. 40°C. 50°D. 45°
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,动点
,动点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 个单位长度的速度沿负方向运动,动点
个单位长度的速度沿负方向运动,动点![]() 从原点出发以每秒
从原点出发以每秒![]() 个单位长度的速度沿负方向运动,动点
个单位长度的速度沿负方向运动,动点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 个单位的速度先沿正方向运动,到达原点后立即按原速反方向运动,三点同时出发,出发时间为
个单位的速度先沿正方向运动,到达原点后立即按原速反方向运动,三点同时出发,出发时间为![]() (秒).
(秒).

(1)点![]() 在数轴上所表示的数分别为:____________,____________;
在数轴上所表示的数分别为:____________,____________;
(2)当![]() 两点重合时,求此时点
两点重合时,求此时点![]() 在数轴上所表示的数;
在数轴上所表示的数;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在3×3的方格中,每行、每列及对角线上的3个代数式的和都相等,我们把这样的方格图叫做“等和格”。如图的“等和格”中,每行、每列及对角线上的3个代数式的和都等于15.
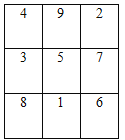
(1)图1是显示部分代数式的“等和格”,可得a=_______(含b的代数式表示);
(2)图2是显示部分代数式的“等和格”,可得a=__________,b=__________;
(3)图3是显示部分代数式的“等和格”,求b的值。(写出具体求解过程)
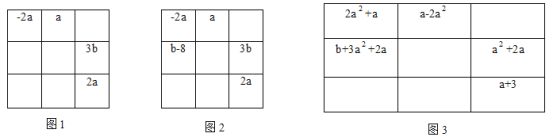
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分6分)某公司调查某中学学生对其环保产品的了解情况,随机抽取该校部分学生进行问卷,结果分“非常了解”、“比较了解”、“一般了解”、“不了解”四种类型,分别记为A、B、C、D.根据调查结果绘制了如下尚不完整的统计图. 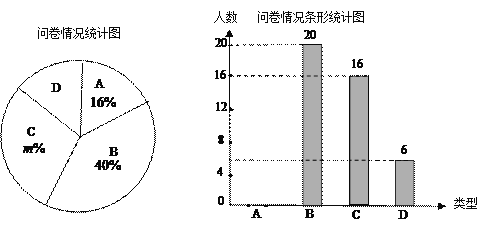
(1)本次问卷共随机调查了 名学生,扇形统计图中m= .
(2)请根据数据信息补全条形统计图;
(3)若该校有1000名学生,估计选择“非常了解”、“比较了解”共约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
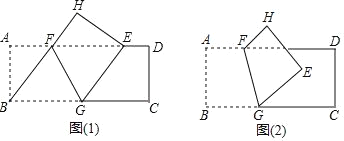
【题目】如图,长方形纸片ABCD中,AB=8,将纸片折叠,折痕的一个端点F在边AD上,另一个端点G在边BC上,顶点B的对应点为E.
(1)如图(1),当顶点B的对应点E落在边AD上时.
①连接BF,试判断四边形BGEF是怎样的特殊四边形,并说明理由;
②若BG=10,求折痕FG的长;
(2)如图(2),当顶点B的对应点E落在长方形内部,E到AD的距离为2,且BG=10时,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知直线AB经过点A(﹣2,0),与y轴的正半轴交于点B,且OA=2OB.
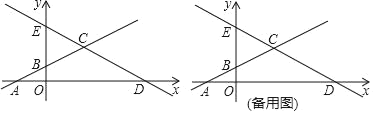
(1)求直线AB的函数表达式;
(2)点C在直线AB上,且BC=AB,点E是y轴上的动点,直线EC交x轴于点D,设点E的坐标为(0,m)(m>2),求点D的坐标(用含m的代数式表示);
(3)在(2)的条件下,若CE:CD=1:2,点F是直线AB上的动点,在直线AC上方的平面内是否存在一点G,使以C,G,F,E为顶点的四边形是菱形?若存在,请求出点G的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
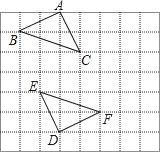
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,△ABC与△DEF关于点O成中心对称,△ABC与△DEF的顶点均在格点上.
(1)在图中直接画出O点的位置;
(2)若以O点为平面直角坐标系的原点,线段AD所在的直线为y轴,过点O垂直AD的直线为x轴,此时点B的坐标为(﹣2,2),请你在图上建立平面直角坐标系,并回答下面的问题:将△ABC先向右平移4个单位长度,再向下平移2个单位长度,得到△A1B1C1,请画出△A1B1C1,并直接写出点B1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有三个点A,B,C,回答下列问题:
(1)若将点B向右移动6个单位后,三个点所表示的数中最小的数是多少?
(2)在数轴上找一点D,使点D到A,C两点的距离相等,写出点D表示的数;
(3)在点B左侧找一点E,使点E到点A的距离是到点B的距离的2倍,并写出点E表示的数.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(新定义):A、B、C 为数轴上三点,若点 C 到 A 的距离是点 C 到 B 的距离的 3 倍,我们就称点
C 是(A,B)的幸运点.
(特例感知):
(1)如图 1,点 A 表示的数为﹣1,点 B 表示的数为 3.表示 2 的点 C 到点 A 的距离是 3, 到点 B 的距离是 1,那么点 C 是(A,B)的幸运点.
①(B,A)的幸运点表示的数是 ;A.﹣1; B.0; C.1; D.2
②试说明 A 是(C,E)的幸运点.
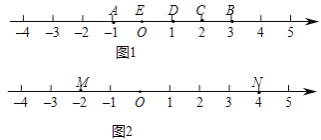
(2)如图 2,M、N 为数轴上两点,点 M 所表示的数为﹣2,点 N 所表示的数为 4,则(M,N)的幸点示的数为 .
(拓展应用):
(3)如图 3,A、B 为数轴上两点,点 A 所表示的数为﹣20,点 B 所表示的数为 40.现有一只电子蚂蚁 P 从点 B 出发,以 3 个单位每秒的速度向左运动,到达点 A 停止.当 t 为何值时,P、A 和 B 三个点中恰好有一个点为其余两点的幸运点?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com