
【题目】定义:底与腰的比是![]() 的等腰三角形叫做黄金等腰三角形.
的等腰三角形叫做黄金等腰三角形.
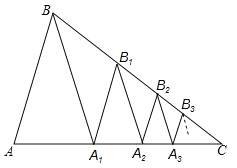
如图,已知△ABC中,AB=BC,∠C=36°,BA1平分∠ABC交AC于A1.
(1)![]() =AA1A C;
=AA1A C;
(2)探究:△ABC是否为黄金等腰三角形?请说明理由;(提示:此处不妨设AC=1)
(3)应用:已知AC=a,作A1B1∥AB交BC于B1,B1A2平分∠A1B1C交AC于A2,作A2B2∥AB交B2,B2A3平分∠A2B2C交AC于A3,作A3B3∥AB交BC于B3,…,依此规律操作下去,用含a,n的代数式表示An﹣1An.(n为大于1的整数,直接回答,不必说明理由)

【答案】(1)证明见试题解析;(2)△ABC是黄金等腰三角形;(3)![]() .
.
【解析】
试题分析:(1)由角平分线的性质和相似三角形的判定与性质,得到△ABC∽△AA1B,从而有![]() ,求出即可;
,求出即可;
(2)设AC=1,则AB2=1﹣AB,求出AB的值,进而得出![]() =
=![]() ,即可得出结论;
,即可得出结论;
(3)利用(2)中所求进而得出AA1,A1A2的长,进而得出其长度变化规律求出即可.
试题解析:(1)∵AC=BC,∠C=36°,∴∠A=∠ABC=72°,∵BA1平分∠ABC,∴∠ABA1=![]() ∠ABC=36°,∴∠C=∠ABA1,又∵∠A=∠A,∴△ABC∽△AA1B,∴
∠ABC=36°,∴∠C=∠ABA1,又∵∠A=∠A,∴△ABC∽△AA1B,∴![]() ,即
,即![]() =AA1A C;
=AA1A C;
(2)△ABC是黄金等腰三角形,理由:
由(1)知,![]() =AA1A C,设AC=1,∴
=AA1A C,设AC=1,∴![]() =AA1,又由(1)可得:AB=A1B,∵∠A1BC=∠C=36°,∴A1B=A1C,∴AB=A1C,∴AA1=AC﹣A1C=AC﹣AB=1﹣AB,∴
=AA1,又由(1)可得:AB=A1B,∵∠A1BC=∠C=36°,∴A1B=A1C,∴AB=A1C,∴AA1=AC﹣A1C=AC﹣AB=1﹣AB,∴![]() =1﹣AB,设AB=x,即
=1﹣AB,设AB=x,即![]() ,∴
,∴![]() ,解得:
,解得:![]() ,
,![]() (不合题意舍去),∴AB=
(不合题意舍去),∴AB=![]() ,又∵AC=1,∴
,又∵AC=1,∴![]() =
=![]() ,∴△ABC是黄金等腰三角形;
,∴△ABC是黄金等腰三角形;
(3)由(2)得;当AC=a,则AA1=AC﹣A1C=AC﹣AB=a﹣AB=![]() =
=![]() ,
,
同理可得:A1A2=A1C﹣A1B1=AC﹣AA1﹣A1B1
=![]() =
=![]() =
=![]() ;
;
故An﹣1An=![]() .
.


科目:初中数学 来源: 题型:
【题目】乘法公式的探究及应用.
(1)如图1可以求出阴影部分的面积是(写成两数平方差的形式);
(2)如图2若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 , 长是 , 面积是(写成多项式乘法的形式);
(3)比较图1、图2两图的阴影部分面积,可以得到乘法公式 (用式子表达);
(4)运用你所得到的公式,计算下列各题:
①(2m+n﹣p)(2m﹣n+p)
②10.3×9.7.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列从左到右的变形,是分解因式的为( )
A. x2﹣2x+1=x(x﹣2)+1 B. a(a﹣b)=a2﹣ab C. x2﹣x=x(x﹣1) D. (a+3)(a﹣3)=a2﹣9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( ) 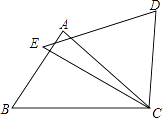
A.BC=EC,∠B=∠E
B.BC=EC,AC=DC
C.BC=EC,∠A=∠D
D.∠B=∠E,∠A=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,若有下列四个条件:①AB//CD;②AD=BC;③∠A=∠C;④AB=CD,现以其中的两个条件为一组,能判定四边形ABCD是平行四边形的条件有 ( )
A. 3组 B. 4组 C. 5组 D. 6组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品经过连续两次降价,销售单价由原来200元降到168元.设平均每次降价的百分率为x,根据题意可列方程为( )
A.200(1﹣x)2=168B.200(1+x)2=168
C.168(1+x)2=200D.168(1﹣x)2=200
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com