
【题目】在△ABC中,AC=AB=5,一边上高为3,求底边BC的长(注意:请画出图形).
【答案】解:分三种情况:①当底边BC边上的高为3时,如图1所示,
∵在△ACD中,AB=AC=5,高AD=3,
∴BD=CD= ![]() =4,
=4,
∴BC=2BD=8;
②当腰上的高BD=3时,如图2所示:
则AD= ![]() =4,
=4,
∴CD=5﹣4=1,
∴BC= ![]() =
= ![]() =
= ![]() ;
;
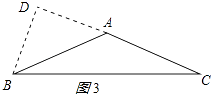
③当高在△ABC的外部时,如图3所示:
∵在△BCD中,AB=AC=5,高BD=3,
∴AD= ![]() =4,
=4,
∴CD=4+5=9,
∴BC= ![]() =
= ![]() =3
=3 ![]() ;
;
综上所述:底边BC的长是8或 ![]() 或3
或3 ![]() .
.


【解析】分三种情况:①当底边BC边上的高为3时;②当腰上的高BD=3时;③当高在△ABC的外部时;根据勾股定理先求得AD,根据线段的和差求得BD,根据勾股定理求得底边BC的长.
【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识,掌握等腰三角形的两个底角相等(简称:等边对等角),以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°. 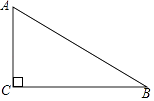
(1)用尺规在边BC上求作一点P,使PA=PB(不写作法,保留作图痕迹);
(2)连结AP,若AC=4,BC=8时,试求点P到AB边的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:底与腰的比是![]() 的等腰三角形叫做黄金等腰三角形.
的等腰三角形叫做黄金等腰三角形.
如图,已知△ABC中,AB=BC,∠C=36°,BA1平分∠ABC交AC于A1.
(1)![]() =AA1A C;
=AA1A C;
(2)探究:△ABC是否为黄金等腰三角形?请说明理由;(提示:此处不妨设AC=1)
(3)应用:已知AC=a,作A1B1∥AB交BC于B1,B1A2平分∠A1B1C交AC于A2,作A2B2∥AB交B2,B2A3平分∠A2B2C交AC于A3,作A3B3∥AB交BC于B3,…,依此规律操作下去,用含a,n的代数式表示An﹣1An.(n为大于1的整数,直接回答,不必说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各组中的四条线段成比例的是( )
A.1cm、2cm、20cm、30cm
B.1cm、2cm、3cm、4cm
C.5cm、10cm、10cm、20cm
D.4cm、2cm、1cm、3cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长为1的网格中,A,E为格点,B,F为小正方形边的中点,C为AE,BF的延长线的交点.
(1)AE的长等于________;
(2)若点P在线段AC上,点Q在线段BC上,且满足AP = PQ = QB,请在如图所示的网格中,用无刻度的直尺,画出线段PQ,并简要说明点P,Q的位置是如何找到的(不要求证明)________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com