
【题目】如图,抛物线y=ax2+bx-3与![]() 轴交于
轴交于![]() ,
,![]() 两点(
两点(![]() 点在
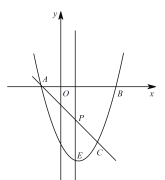
点在![]() 点左侧),A(-1,0),B(3,0),直线
点左侧),A(-1,0),B(3,0),直线![]() 与抛物线交于
与抛物线交于![]() ,
,![]() 两点,其中
两点,其中![]() 点的横坐标为
点的横坐标为![]() 。
。
(1)求抛物线的函数解析式;
(2)![]() 是线段
是线段![]() 上的一个动点,过
上的一个动点,过![]() 点作
点作![]() 轴的平行线交抛物线于
轴的平行线交抛物线于![]() 点,求线段
点,求线段![]() 长度的最大值;
长度的最大值;
(3)点![]() 是抛物线上的动点,在
是抛物线上的动点,在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() ,
,![]() ,
,![]() ,
,![]() 这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的
这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的![]() 点坐标;如果不存在,请说明理由。
点坐标;如果不存在,请说明理由。
【答案】(1)y=x2﹣2x﹣3;(2)![]() ;(3)存在4个符合条件的F点,分别为F(﹣3,0),(1,0),(4+
;(3)存在4个符合条件的F点,分别为F(﹣3,0),(1,0),(4+![]() ,0),(4﹣
,0),(4﹣![]() ,0).
,0).
【解析】
(1)将A、B的坐标代入抛物线中,易求出抛物线的解析式;
(2)将C点横坐标代入抛物线的解析式中,即可求出C点的坐标.由待定系数法可求出直线AC的解析式.PE的长实际是直线AC与抛物线的函数值的差,可设P点的横坐标为x,用x分别表示出P、E的纵坐标,即可得到关于PE的长、x的函数关系式,根据所得函数的性质即可求得PE的最大值;
(3)此题要分两种情况:①以AC为边,②以AC为对角线.确定平行四边形后,可直接利用平行四边形的性质求出F点的坐标.
(1)将A(﹣1,0),B(3,0)代入y=ax2+bx-3,得:a=1,b=﹣2,∴y=x2﹣2x﹣3.
(2)将C点的横坐标x=2代入y=x2﹣2x﹣3,得:y=﹣3,∴C(2,﹣3),∴直线AC的函数解析式是y=﹣x﹣1.
设P点的横坐标为x(﹣1≤x≤2),则P、E的坐标分别为:P(x,﹣x﹣1),E(x,x2﹣2x﹣3).
∵P点在E点的上方,∴PE=(﹣x﹣1)﹣(x2﹣2x﹣3)=﹣x2+x+2,∴当x=![]() 时,PE的最大值=
时,PE的最大值=![]() .
.
(3)存在.讨论如下:
①如图,连接C与抛物线和y轴的交点.
∵C(2,﹣3),G(0,﹣3),∴CG∥x轴,此时AF=CG=2,∴F点的坐标是(﹣3,0);

②如图,AF=CG=2,A点的坐标为(﹣1,0),因此F点的坐标为(1,0);

③如图,设F(x,0).
∵ACFG是平行四边形,∴AF的中点与CG的中点重合.
∵AF的中点的纵坐标为0,∴C,G两点的纵坐标互为相反数,∴G点的纵坐标为3,∴x2﹣2x﹣3=3,解得:x=1±![]() ,∴G点的坐标为(1±
,∴G点的坐标为(1±![]() ,3),∴AF的中点的横坐标=CG的中点的横坐标,∴
,3),∴AF的中点的横坐标=CG的中点的横坐标,∴![]() ,解得:x=
,解得:x=![]() ,∴F的坐标为(
,∴F的坐标为(![]() ,0).
,0).


综上所述:存在4个符合条件的F点,分别为F(﹣3,0),(1,0),(4+![]() ,0),(4﹣
,0),(4﹣![]() ,0).
,0).


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=![]() x+3的图象分别与y轴,x轴交于点A,B,点P从点B出发,沿射线BA以每秒1个单位的速度运动,设点P的运动时间为t秒.
x+3的图象分别与y轴,x轴交于点A,B,点P从点B出发,沿射线BA以每秒1个单位的速度运动,设点P的运动时间为t秒.

(1)点P在运动过程中,若某一时刻,△OPA的面积为3,求此时P的坐标;
(2)在整个运动过程中,当t为何值时,△AOP为等腰三角形?请直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上的动点(
边上的动点(![]() 不与
不与![]() 、
、![]() 重合),
重合),![]()

![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
(1)![]() 与
与![]() 的大小关系为________.请证明你的结论;
的大小关系为________.请证明你的结论;
(2)设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的长;
的长;
(4)是否存在![]() ,使
,使![]() 的面积是
的面积是![]() 面积的
面积的![]() 倍?若存在,求出
倍?若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形 ![]() 是菱形,
是菱形,![]() B=6,且∠ABC=60° ,M是菱形内任一点,连接AM,BM,CM,则AM+BM+CM 的最小值为________。
B=6,且∠ABC=60° ,M是菱形内任一点,连接AM,BM,CM,则AM+BM+CM 的最小值为________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种饮料,平均每天可售出100箱,每箱利润120元.为了扩大销售,增加利润,超市准备适当降价.据测算,若每箱降价1元,每天可多售出2箱.
(1)如果要使每天销售饮料获利14000元,问每箱应降价多少元?
(2)每箱降价多少元超市每天获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个矩形的短边与长边的比值为![]() (黄金分割数),我们把这样的矩形叫做黄金矩形.
(黄金分割数),我们把这样的矩形叫做黄金矩形.
![]() 操作:请你在如图所示的黄金矩形
操作:请你在如图所示的黄金矩形![]() 中,以短边
中,以短边![]() 为一边作正方形
为一边作正方形![]() ;
;
![]() 探究:在
探究:在![]() 中的四边形
中的四边形![]() 是不是黄金矩形?若是,请予以证明;若不是,请说明理由.
是不是黄金矩形?若是,请予以证明;若不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=![]() ,BC=6cm,AC=10cm。
,BC=6cm,AC=10cm。
(1)求AB的长;
(2)若P点从点B出发,以2cm/s的速度在BC所在的直线![]() 上运动,设运动时间为t秒,那么当t为何值时,△ACP为等腰三角形。
上运动,设运动时间为t秒,那么当t为何值时,△ACP为等腰三角形。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】锐锐参加我市电视台组织的“牡丹杯”智力竞答节目,答对最后两道单选题就顺利通关,第一道单选题有3个选项,第二道单选题有4个选项,这两道题锐锐都不会,不过锐锐还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).
(1)如果锐锐两次“求助”都在第一道题中使用,那么锐锐通关的概率是________;
(2)如果锐锐两次“求助”都在第二道题中使用,那么锐锐通关的概率是________;
(3)如果锐锐每道题各用一次“求助”,请用树状图或者列表来分析他顺利通关的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮计划暑期结伴参加志愿者活动.小明想参加敬老服务活动,小亮想参加文明礼仪宣传活动.他们想通过做游戏来决定参加哪个活动,于是小明设计了一个游戏,游戏规则是:在三张完全相同的卡片上分别标记4、5、6三个数字,一人先从三张卡片中随机抽出一张,记下数字后放回,另一人再从中随机抽出一张,记下数字,若抽出的两张卡片标记的数字之和为偶数,则按照小明的想法参加敬老服务活动,若抽出的两张卡片标记的数字之和为奇数,则按照小亮的想法参加文明礼仪宣传活动.你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com