
ЁОЬтФПЁПЮЪЬтЬсГі
ЃЈ1ЃЉШчЭМ1ЃЌе§ЗНаЮABCDЕФЖдНЧЯпНЛгкЕуOЃЌЁїCDEЪЧБпГЄЮЊ6ЕФЕШБпШ§НЧаЮЃЌдђOЁЂEжЎМфЕФОрРыЮЊ ЃЛ
ЮЪЬтЬНОП
ЃЈ2ЃЉШчЭМ2ЃЌдкБпГЄЮЊ6ЕФе§ЗНаЮABCDжаЃЌвдCDЮЊжБОЖзїАыдВOЃЌЕуPЮЊЛЁCDЩЯвЛЖЏЕуЃЌЧѓAЁЂPжЎМфЕФзюДѓОрРыЃЛ
ЮЪЬтНтОі
ЃЈ3ЃЉвЄЖДЪЧЮвЪЁЩТББХЉДхЕФжївЊНЈжўЃЌвЄЖДБіЙнИќЪЧвЛЕРіІРіЕФЗчОАЯпЃЌЪЧвђЮЊвЄЖДГ§СЫЫќЕФМсЙЬадМАЬигаЕФЭтдкУРжЎЭтЃЌЛЙОпгаЖЌХЏЯФСЙЕФЬьШЛгХЕуМвзЁбгАВХЉДхЕФвЛЖдМДНЋВЮМгжаПМЕФЫЋАћЬЅаЁБІКЭаЁБДСНажЕмЃЌЗЂЯжздМвЕФвЄЖД(ШчЭМ3ЫљЪО)ЕФУХДАЪЧгЩОиаЮABCDМАЙаЮAMDзщГЩЃЌAB=2mЃЌBC=3.2mЃЌЙИпMN=1.2m(NЮЊADЕФжаЕуЃЌMNЁЭAD)ЃЌаЁБІЫЕЃЌУХНЧBЕНУХДАЙаЮЛЁADЕФзюДѓОрРыЪЧBЁЂMжЎМфЕФОрРыЃЎаЁБДЫЕетВЛЪЧзюДѓЕФОрРыЃЌФуШЯЮЊЫЕФЫЕЗЈе§ШЗЃПЧыЭЈЙ§МЦЫуЧѓГіУХНЧBЕНУХДАЙаЮЛЁADЕФзюДѓОрРыЃЎ

ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ2ЃЉаЁБДЕФЫЕЗЈе§ШЗЃЌРэгЩМћНтЮіЃЌ
ЃЛЃЈ2ЃЉаЁБДЕФЫЕЗЈе§ШЗЃЌРэгЩМћНтЮіЃЌ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉСЌНгACЃЌBDЃЌгЩOEДЙжБЦНЗжDCПЩЕУDHГЄЃЌвзжЊOHЁЂHEГЄЃЌЯрМгМДПЩЃЛ
ЃЈ2ЃЉВЙШЋЁбOЃЌСЌНгAOВЂбгГЄНЛЁбOгвАыВргкЕуPЃЌдђДЫЪБAЁЂPжЎМфЕФОрРызюДѓЃЌдкRtЁїAODжаЃЌгЩЙДЙЩЖЈРэПЩЕУAOГЄЃЌвзЧѓAPГЄЃЛ
ЃЈ3ЃЉаЁБДЕФЫЕЗЈе§ШЗЃЌВЙШЋЙаЮЛЁADЫљдкЕФЁбOЃЌСЌНгONЃЌOAЃЌODЃЌЙ§ЕуOзїOEЁЭABгкЕуEЃЌСЌНгBOВЂбгГЄНЛЁбOЩЯЖЫгкЕуPЃЌдђДЫЪБBЁЂPжЎМфЕФОрРыМДЮЊУХНЧBЕНУХДАЙаЮЛЁADЕФзюДѓОрРыЃЌдкRtЁїANOжаЃЌЩшAO=rЃЌгЩЙДЙЩЖЈРэПЩЧѓГіrЃЌдкRtЁїOEBжаЃЌгЩЙДЙЩЖЈРэПЩЕУBOГЄЃЌвзжЊBPГЄ.
НтЃКЃЈ1ЃЉШчЭМ1ЃЌСЌНгACЃЌBDЃЌЖдНЧЯпНЛЕуЮЊOЃЌСЌНгOEНЛCDгкHЃЌдђOD=OCЃЎ
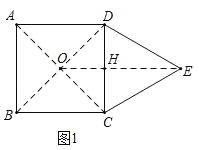
ЁпЁїDCEЮЊЕШБпШ§НЧаЮЃЌ
ЁрED=ECЃЌ
ЁпOD=OC
ЁрOEДЙжБЦНЗжDCЃЌ
ЁрDH![]() DC=3ЃЎ
DC=3ЃЎ
ЁпЫФБпаЮABCDЮЊе§ЗНаЮЃЌ
ЁрЁїOHDЮЊЕШбќжБНЧШ§НЧаЮЃЌ
ЁрOH=DH=3ЃЌ
дкRtЁїDHEжаЃЌ
HE![]() DH=3
DH=3![]() ЃЌ
ЃЌ
ЁрOE=HE+OH=3![]() 3ЃЛ
3ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌВЙШЋЁбOЃЌСЌНгAOВЂбгГЄНЛЁбOгвАыВргкЕуPЃЌдђДЫЪБAЁЂPжЎМфЕФОрРызюДѓЃЌ
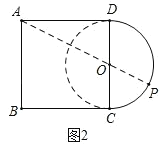
дкRtЁїAODжаЃЌAD=6ЃЌDO=3ЃЌ
ЁрAO![]() 3
3![]() ЃЌ
ЃЌ
![]()
ЁрAP=AO+OP=3![]() 3ЃЛ
3ЃЛ
ЃЈ3ЃЉаЁБДЕФЫЕЗЈе§ШЗЃЎРэгЩШчЯТЃЌ
ШчЭМ3ЃЌВЙШЋЙаЮЛЁADЫљдкЕФЁбOЃЌСЌНгONЃЌOAЃЌODЃЌЙ§ЕуOзїOEЁЭABгкЕуEЃЌСЌНгBOВЂбгГЄНЛЁбOЩЯЖЫгкЕуPЃЌдђДЫЪБBЁЂPжЎМфЕФОрРыМДЮЊУХНЧBЕНУХДАЙаЮЛЁADЕФзюДѓОрРыЃЌ
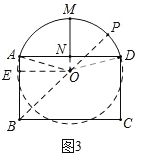
гЩЬтвтжЊЃЌЕуNЮЊADЕФжаЕуЃЌ![]() ЃЌ
ЃЌ
ЁрAN![]() AD=1.6ЃЌONЁЭADЃЌ
AD=1.6ЃЌONЁЭADЃЌ
дкRtЁїANOжаЃЌ
ЩшAO=rЃЌдђON=rЉ1.2ЃЎ
ЁпAN2+ON2=AO2ЃЌ
Ёр1.62+(rЉ1.2)2=r2ЃЌ
НтЕУЃКr![]() ЃЌ
ЃЌ
ЁрAE=ON![]() 1.2
1.2![]() ЃЌ
ЃЌ
дкRtЁїOEBжаЃЌOE=AN=1.6ЃЌBE=ABЉAE![]() ЃЌ
ЃЌ
ЁрBO![]() ЃЌ
ЃЌ
ЁрBP=BO+PO![]() ЃЌ
ЃЌ
ЁрУХНЧBЕНУХДАЙаЮЛЁADЕФзюДѓОрРыЮЊ![]() ЃЎ
ЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭЏРЯЪІМЦЛЎЙКТђAЁЂBСНжжБЪМЧБОЙВ30БОзїЮЊАрЛсНБЦЗЃЌетСНжжБЪМЧБОЕФЕЅМлЗжБ№ЪЧ12дЊКЭ8дЊЃЌВЂЧвЙКТђЕФAжжБЪМЧБОЕФЪ§СПвЊЩйгкBжжБЪМЧБОЪ§СПЕФ![]() ЃЌЕЋгжВЛЩйгкBжжБЪМЧБОЪ§СПЕФ
ЃЌЕЋгжВЛЩйгкBжжБЪМЧБОЪ§СПЕФ![]() ЃЎШчЙћЩшТђAжжБЪМЧБОxБОЃЌТђетСНжжБЪМЧБОЙВЛЈЗбyдЊЃЎ
ЃЎШчЙћЩшТђAжжБЪМЧБОxБОЃЌТђетСНжжБЪМЧБОЙВЛЈЗбyдЊЃЎ
ЃЈ1ЃЉЧѓМЦЛЎЙКТђетСНжжБЪМЧБОЫљашЕФЗбгУyЃЈдЊЃЉЙигкxЃЈБОЃЉЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЭЏРЯЪІгаЖрЩйжжВЛЭЌЕФЙКТђЗНАИЃП
ЃЈ3ЃЉЩЬЕъЮЊСЫДйЯњЃЌОіЖЈЖдAжжБЪМЧБОУПБОШУРћaЃЈ4ЃМaЁм7ЃЉдЊЯњЪлЃЌBжжБЪМЧБОУПБОШУРћbдЊЯњЪлЃЌЭЏРЯЪІЗЂЯжЙКТђЫљашЕФзмЗбгУгыЙКТђЕФЗНАИЮоЙиЃЎЕБзмЗбгУзюЩйЪБЃЌЧѓДЫЪБaЁЂbЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгаЫФеХНівЛУцЗжБ№Бъга1ЃЌ2ЃЌ3ЃЌ4ЕФВЛЭИУїжНЦЌЃЌГ§ЫљБъЪ§зжВЛЭЌЭтЃЌЦфгрЖМЭъШЋЯрЭЌЃЎ
ЃЈ1ЃЉНЋЫФеХжНЦЌЗжГЩСНзщЃЌБъга1ЁЂ3ЕФЮЊЕквЛзщЃЌБъга2ЁЂ4ЕФЮЊЕкЖўзщЃЌБГУцЯђЩЯЃЌЗХдкзРЩЯЃЌДгСНзщжаИїЫцЛњГщШЁвЛеХЃЌЧѓСНДЮГщШЁЪ§зжКЭЮЊ5ЕФИХТЪЃЛ
ЃЈ2ЃЉНЋЫФеХжНЦЌЯДдШКѓБГУцЯђЩЯЃЌЗХдкзРЩЯЃЌвЛДЮадДгжаЫцЛњГщШЁСНеХЃЌгУЪїаЮЭМЗЈЛђСаБэЗЈЃЌЧѓЫљГщШЁЪ§зжКЭЮЊ5ЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
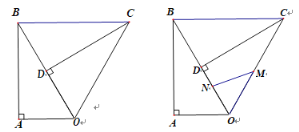
ЁОЬтФПЁПвбжЊRtЁїOABЃЌOAB90ЃЌABO30ЃЌаББпOB4ЃЌНЋRtЁїOABШЦЕуOЫГЪБеыа§зЊ60ЃЌЕУЕНЁїCODЃЌШчЭМ1ЃЌСЌНгBCЃЎ
ЃЈ1ЃЉЧѓBCЕФГЄЖШЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕуMЃЌNЭЌЪБДгЕуOГіЗЂЃЌдкЁїOCBБпЩЯдЫЖЏЃЌMбиOCBТЗОЖдШЫйдЫЖЏЃЌNбиOBCТЗОЖдШЫйдЫЖЏЃЌЕБСНЕуЯргіЪБдЫЖЏЭЃжЙЃЌвбжЊЕуMЕФдЫЖЏЫйЖШЮЊ1.5ИіЕЅЮЛ/УыЃЌЕуNЕФдЫЖЏЫйЖШЮЊ1ИіЕЅЮЛ/УыЃЌЩшдЫЖЏЪБМфЮЊxУыЃЌЁїOMNЕФУцЛ§ЮЊyЃЌЧѓyЙигкxЕФКЏЪ§НтЮіЪНЃЌВЂжБНгаДГіздБфСПxЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ2016ЩНЖЋЪЁбЬЬЈЪаЃЉФГжабЇЙуГЁЩЯгаЦьИЫШчЭМ1ЫљЪОЃЌдкбЇЯАНтжБНЧШ§НЧаЮвдКѓЃЌЪ§бЇаЫШЄаЁзщВтСПСЫЦьИЫЕФИпЖШЃЎШчЭМ2ЃЌФГвЛЪБПЬЃЌЦьИЫABЕФгАзгвЛВПЗжТфдкЦНЬЈЩЯЃЌСэвЛВПЗжТфдкаБЦТЩЯЃЌВтЕУТфдкЦНЬЈЩЯЕФгАГЄBCЮЊ4УзЃЌТфдкаБЦТЩЯЕФгАГЄCDЮЊ3УзЃЌABЁЭBCЃЌЭЌвЛЪБПЬЃЌЙтЯпгыЫЎЦНУцЕФМаНЧЮЊ72ЁуЃЌ1УзЕФЪњСЂБъИЫPQдкаБЦТЩЯЕФгАГЄQRЮЊ2УзЃЌЧѓЦьИЫЕФИпЖШЃЈНсЙћОЋШЗЕН0.1УзЃЉЃЎЃЈВЮПМЪ§ОнЃКsin72ЁуЁж0.95ЃЌcos72ЁуЁж0.31ЃЌtan72ЁуЁж3.08ЃЉ
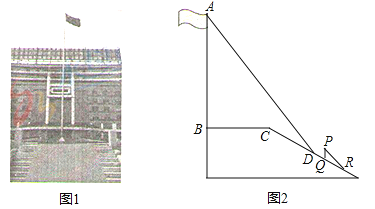
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌФГаЁЧјТЅЗПИННќгавЛИіаБЦТЃЌЦТНЧЮЊ30ЁуЃЌаЁЭѕЗЂЯжТЅЗПдкЫЎЦНЕиУцгыаБЦТДІаЮГЩЕФЭЖгАжаЃЌдкаБЦТЩЯЕФгАзгГЄCD=6mЃЌЦТНХЕНТЅЗПЕФОрРыCB=8mЃЎдкDЕуДІЙлВьЕуAЕФбіНЧЮЊ60ЁуЃЎЧѓТЅЗПABЕФИпЖШЃЈНсЙћБЃСєИљКХЃЉЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ8ЗжЃЉФГЕїВщаЁзщВЩгУМђЕЅЫцЛњГщбљЗНЗЈЃЌЖдФГЪаВПЗжжааЁбЇЩњвЛЬьжабєЙтЬхг§дЫЖЏЪБМфНјааСЫГщбљЕїВщЃЌВЂАбЫљЕУЪ§ОнећРэКѓЛцжЦГЩШчЯТЕФЭГМЦЭМЃК
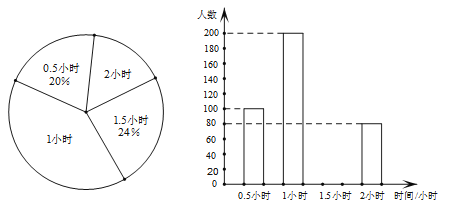
ЃЈ1ЃЉИУЕїВщаЁзщГщШЁЕФбљБОШнСПЪЧЖрЩйЃП
ЃЈ2ЃЉЧѓбљБОбЇЩњжабєЙтЬхг§дЫЖЏЪБМфЮЊ1.5аЁЪБЕФШЫЪ§ЃЌВЂВЙШЋеМЦЕЪ§ЗжВМжБЗНЭМЃЛ
ЃЈ3ЃЉЧыЙРМЦИУЪажааЁбЇЩњвЛЬьжабєЙтЬхг§дЫЖЏЕФЦНОљЪБМфЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгЩЮвЙњЭъШЋзджїЩшМЦЁЂзджїНЈдьЕФЪзЫвЙњВњКНФИгк2018Фъ5дТГЩЙІЭъГЩЕквЛДЮКЃЩЯЪдбщШЮЮё.ШчЭМЃЌКНФИгЩЮїЯђЖЋКНааЃЌЕНДя![]() ДІЪБЃЌВтЕУаЁЕК
ДІЪБЃЌВтЕУаЁЕК![]() ЮЛгкЫќЕФББЦЋЖЋ
ЮЛгкЫќЕФББЦЋЖЋ![]() ЗНЯђЃЌЧвгыКНФИЯрОр80КЃРяЃЌдйКНаавЛЖЮЪБМфКѓЕНДяBДІЃЌВтЕУаЁЕК
ЗНЯђЃЌЧвгыКНФИЯрОр80КЃРяЃЌдйКНаавЛЖЮЪБМфКѓЕНДяBДІЃЌВтЕУаЁЕК![]() ЮЛгкЫќЕФББЦЋЖЋ
ЮЛгкЫќЕФББЦЋЖЋ![]() ЗНЯђ.ШчЙћКНФИМЬајКНаажСаЁЕК
ЗНЯђ.ШчЙћКНФИМЬајКНаажСаЁЕК![]() ЕФе§ФЯЗНЯђЕФ
ЕФе§ФЯЗНЯђЕФ![]() ДІЃЌЧѓЛЙашКНааЕФОрРы
ДІЃЌЧѓЛЙашКНааЕФОрРы![]() ЕФГЄ.
ЕФГЄ.
ЃЈВЮПМЪ§ОнЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDЕФЖдНЧЯпACЁЭAEЃЌЩфЯпEBНЛЩфЯпDCгкЕуFЃЌСЌНсAFЃЌШєAFЃН![]() BFЃЌAEЃН4ЃЌдђBEЕФГЄЮЊ_____ЃЎ
BFЃЌAEЃН4ЃЌдђBEЕФГЄЮЊ_____ЃЎ
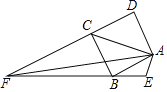
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com