
【题目】如图,在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.
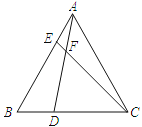
(1)求证:AD=CE;
(2)求∠DFC的度数.
科目:初中数学 来源: 题型:
【题目】为了更好的保护美丽图画的邛海湿地,西昌市污水处理厂决定先购买A、B两型污水处理设备共20台,对邛海湿地周边污水进行处理,每台A型污水处理设备12万元,每台B型污水处理设备10万元.已知1台A型污水处理设备和2台B型污水处理设备每周可以处理污水640吨,2台A型污水处理设备和3台B型污水处理设备每周可以处理污水1080吨.
(1)求A、B两型污水处理设备每周分别可以处理污水多少吨?
(2)经预算,市污水处理厂购买设备的资金不超过230万元,每周处理污水的量不低于4500吨,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】沈阳地铁2号线的开通,方便了市民的出行.从2012年1月9日到2月7日的30天里,累计客运量约达3040000人次,将3040000用科学记数法表示为( )
A.3.04×105
B.3.04×106
C.30.4×105
D.0.304×107
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC≌△DEF,若△ABC的周长为30cm,AB=8cm,BC=12cm,则DE、DF的长度分别是( )
A.8cm和9cmB.8cm和10cmC.10cm和12cmD.8cm和12cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】无论k为何值时,直线y=k(x+3)+4都恒过平面内一个定点,这个定点的坐标为( )
A.(3,4)B.(3,﹣4)C.(﹣3,﹣4)D.(﹣3,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
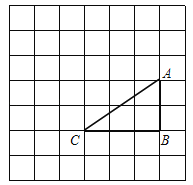
【题目】如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(4,3)、B(4,1),把△ABC绕点C逆时针旋转90°后得到△A1B1C.
(1)画出△A1B1C,直接写出点A1、B1的坐标;
(2)求在旋转过程中,△ABC所扫过的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com