
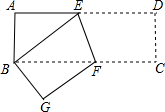
 如图,矩形纸片ABCD的长AD=9cm,宽AB=3cm,沿EF将其折叠,使点D与点B重合,则折痕EF的长为$\sqrt{10}$cm.
如图,矩形纸片ABCD的长AD=9cm,宽AB=3cm,沿EF将其折叠,使点D与点B重合,则折痕EF的长为$\sqrt{10}$cm. 分析 作FM⊥AD于M,则∠FME=90°,FM=AB=3cm,由折叠的性质得出BE=DE,∠BEF=∠DEF,再求出BF=BE,设AE=x,则BE=DE=9-x,根据勾股定理得出方程,解方程求出AE,得出DE、BF、EM,根据勾股定理求出EF即可.
解答 解:作FM⊥AD于M,如图所示: 则∠FME=90°,FM=AB=3cm,
则∠FME=90°,FM=AB=3cm,
根据题意得:BE=DE,∠BEF=∠DEF,
∵四边形ABCD是矩形,
∴∠A=90°,AD∥BC,
∴∠BFE=∠DEF,
∴∠BEF=∠BFE,
∴BF=BE,
设AE=x,则BE=DE=BF=9-x,
根据勾股定理得:
AB2+AE2=BE2,即32+x2=(9-x)2,
解得:x=4,
∴AE=4,
∴DE=BF=5,
∴CF=DM=4,
∴EM=1,
根据勾股定理得:EF=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$(cm);
故答案为:$\sqrt{10}$.
点评 本题考查了翻折变换的性质、矩形的性质、勾股定理、等腰三角形的判定;熟练掌握翻折变换和矩形的性质,并能进行推理计算是解决问题的关键.


科目:初中数学 来源: 题型:解答题
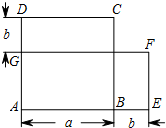 (1)如图,正方形ABCD的边长为a,周长为4a;长方形AEFG的长为a+b,宽为a-b,长为4a.
(1)如图,正方形ABCD的边长为a,周长为4a;长方形AEFG的长为a+b,宽为a-b,长为4a.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
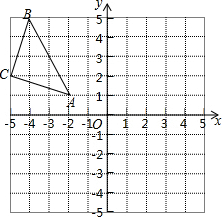 在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-4,5),C(-5,2).
在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-4,5),C(-5,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售量p(件) | P=40-x |
| 销售单价q(元/件) | 当1≤x≤20时,q=20+x 当20<x≤30时,q=40 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
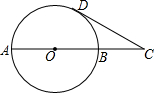 如图,已知AB是⊙O的一条直径,延长AB至C点,使AC=3BC,CD与⊙O相切于D点.若CD=$\sqrt{3}$,则劣弧AD的长为$\frac{2}{3}$π.
如图,已知AB是⊙O的一条直径,延长AB至C点,使AC=3BC,CD与⊙O相切于D点.若CD=$\sqrt{3}$,则劣弧AD的长为$\frac{2}{3}$π.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
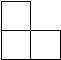 小红在观察由一些相同小立方块搭成的几何体时,发现它的主视图、俯视图、左视图均为如图,则构成该几何体的小立方块的个数有( )
小红在观察由一些相同小立方块搭成的几何体时,发现它的主视图、俯视图、左视图均为如图,则构成该几何体的小立方块的个数有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com