
ЁОЬтФПЁПЮЪЬтЗЂЯж
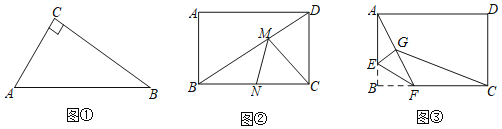
ЃЈ1ЃЉШчЭМЂйЃЌRtЁїABCжаЃЌЁЯCЃН90ЁуЃЌACЃН6ЃЌBCЃН8ЃЌЕуDЪЧABБпЩЯШЮвтвЛЕуЃЌдђCDЕФзюаЁжЕЮЊЁЁ ЁЁЃЛ
ЃЈ2ЃЉШчЭМЂкЃЌОиаЮABCDжаЃЌABЃН6ЃЌBCЃН8ЃЌЕуMЁЂЕуNЗжБ№дкEDЁЂBCЩЯЃЌЧѓCM+MNЕФзюаЁжЕЃЛ
ЃЈ3ЃЉШчЭМЂлЃЎОиаЮABCDжаЃЌABЃН6ЃЌBCЃН8ЃЌЕуEЪЧABБпЩЯвЛЕуЃЌЧвAEЃН4ЃЌЕуFЪЧECБпЩЯЕФШЮвтвЛЕуЃЌАбЁїBEFбиEFЗелЃЌЕуBЕФЖдгІЕуЮЊGЃЌСЌНгAGЁЂCGЃЌЫФБпаЮAGCDЕФУцЛ§ЪЧЗёДцдкзюаЁжЕЃЌШєдкдкЃЌЧѓетИізюаЁжЕМАДЫЪБBFЕФГЄЖШЃЎШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁП(1)![]() ;(2)
;(2)![]() ;(3)МћНтЮі.
;(3)МћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЕуЕНжБЯпЕФОрРызюаЁЃЌдйгУШ§НЧаЮЕФУцЛ§МДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉЯШИљОнжсЖдГЦШЗЖЈГіЕуMКЭNЕФЮЛжУЃЌдйРћгУУцЛ§ЧѓГіCFЃЌНјЖјЧѓГіCEЃЌзюКѓгУШ§НЧКЏЪ§МДПЩЧѓГіCM+MNЕФзюаЁжЕЃЛ
ЃЈ3ЃЉЯШШЗЖЈГіEGЁЭACЪБЃЌЫФБпаЮAGCDЕФУцЛ§зюаЁЃЌдйгУШёНЧШ§НЧКЏЪ§ЧѓГіЕуGЕНACЕФОрРыЃЌзюКѓгУУцЛ§жЎКЭМДПЩЕУГіНсТлЃЌдйгУЯрЫЦШ§НЧаЮЕУГіЕФБШР§ЪНЧѓГіCFМДПЩЧѓГіBFЃЎ
НтЃКЃЈ1ЃЉШчЭМЂйЃЌЙ§ЕуCзїCDЁЭABгкDЃЌИљОнЕуЕНжБЯпЕФОрРыДЙЯпЖЮзюаЁЃЌДЫЪБCDзюаЁЃЌ

дкRtЁїABCжаЃЌACЃН6ЃЌBCЃН8ЃЌИљОнЙДЙЩЖЈРэЕУЃЌABЃН10ЃЌ
Ёп![]() ACЁСBCЃН
ACЁСBCЃН![]() ABЁСCDЃЌ
ABЁСCDЃЌ
ЁрCDЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМЂкЃЌзїГіЕуCЙигкBDЕФЖдГЦЕуEЃЌЙ§ЕуEзїENЁЭBCгкNЃЌНЛBDгкMЃЌСЌНгCMЃЌДЫЪБCM+MNЃНENзюаЁЃЛ

ЁпЫФБпаЮABCDЪЧОиаЮЃЌ
ЁрЁЯBCDЃН90ЁуЃЌCDЃНABЃН6ЃЌИљОнЙДЙЩЖЈРэЕУЃЌBDЃН10ЃЌ
ЁпCEЁЭBCЃЌ
Ёр![]() BDЁСCFЃН
BDЁСCFЃН![]() BCЁСCDЃЌ
BCЁСCDЃЌ
ЁрCFЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
гЩЖдГЦЕУЃЌCEЃН2CFЃН![]() ЃЌ
ЃЌ
дкRtЁїBCFжаЃЌcosЁЯBCFЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрsinЁЯBCFЃН![]() ЃЌ
ЃЌ
дкRtЁїCENжаЃЌENЃНCEsinЁЯBCEЃН![]() ЃН
ЃН![]() ЃЛ
ЃЛ
МДЃКCM+MNЕФзюаЁжЕЮЊЃК![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌ

ЁпЫФБпаЮABCDЪЧОиаЮЃЌ
ЁрCDЃНABЃН6ЃЌADЃНBCЃН8ЃЌЁЯABCЃНЁЯDЃН90ЁуЃЌИљОнЙДЙЩЖЈРэЕУЃЌACЃН10ЃЌ
ЁпABЃН6ЃЌAEЃН4ЃЌ
ЁрЕуFдкBCЩЯЕФШЮКЮЮЛжУЪБЃЌЕуGЪМжедкACЕФЯТЗНЃЌ
ЩшЕуGЕНACЕФОрРыЮЊhЃЌ
ЁпSЫФБпаЮAGCDЃНSЁїACD+SЁїACGЃН![]() ADЁСCD+
ADЁСCD+![]() ACЁСhЃН
ACЁСhЃН![]() ЁС8ЁС6+
ЁС8ЁС6+![]() ЁС10ЁСhЃН5h+24ЃЌ
ЁС10ЁСhЃН5h+24ЃЌ
ЁрвЊЫФБпаЮAGCDЕФУцЛ§зюаЁЃЌМДЃКhзюаЁЃЌ
ЁпЕуGЪЧвдЕуEЮЊдВаФЃЌBEЃН2ЮЊАыОЖЕФдВЩЯдкОиаЮABCDФкВПЕФвЛВПЗжЕуЃЌ
ЁрEGЁЭACЪБЃЌhзюаЁЃЌ
гЩелЕўжЊЁЯEGFЃНЁЯABCЃН90ЁуЃЌ
бгГЄEGНЛACгкHЃЌдђEHЁЭACЃЌ
дкRtЁїABCжаЃЌsinЁЯBACЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
дкRtЁїAEHжаЃЌAEЃН4ЃЌsinЁЯBACЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрEHЃН![]() AEЃН
AEЃН![]() ЃЌ
ЃЌ
ЁрhЃНEHЉEGЃН![]() Љ2ЃН
Љ2ЃН![]() ЃЌ
ЃЌ
ЁрSЫФБпаЮAGCDзюаЁЃН5h+24ЃН5ЁС![]() +24ЃН30ЃЌ
+24ЃН30ЃЌ
Й§ЕуFзїFMЁЭACгкMЃЌ
ЁпEHЁЭFGЃЌEHЁЭACЃЌ
ЁрЫФБпаЮFGHMЪЧОиаЮЃЌ
ЁрFMЃНGHЃН![]()
ЁпЁЯFCMЃНЁЯACBЃЌЁЯCMFЃНCBAЃН90ЁуЃЌ
ЁрЁїCMFЁзЁїCBAЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌ
ЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрCFЃН2ЃЌ
ЁрBFЃНBCЉCFЃН8Љ2ЃН6ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
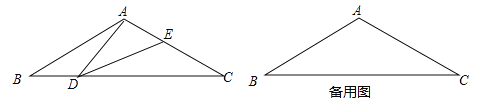
ЁОЬтФПЁПШчЭМЃЌдкЕШбќШ§НЧаЮABCжаЃЌЁЯBAC=120ЁуЃЌAB=AC=2ЃЌЕуDЪЧBCБпЩЯЕФвЛИіЖЏЕуЃЈВЛгыBЁЂCжиКЯЃЉЃЌдкACЩЯШЁвЛЕуEЃЌЪЙЁЯADE=30ЁуЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїABDЁзЁїDCEЃЛ
ЃЈ2ЃЉЩшBD=xЃЌAE=yЃЌЧѓyЙигкxЕФКЏЪ§ЙиЯЕЪНВЂаДГіздБфСПxЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌDЪЧЕШБпЁїABCБпABЩЯЕФвЛЕуЃЌЧвADЃКDBЃН1ЃК2ЃЌЯжНЋЁїABCелЕўЃЌЪЙЕуCгыDжиКЯЃЌелКлЮЊEFЃЌЕуEЁЂFЗжБ№дкACКЭBCЩЯЃЌдђCEЃКCFЕФжЕЮЊЃЈЁЁЁЁ ЃЉ

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊШчЭМЃЌЖўДЮКЏЪ§![]() ЕФЭМЯѓОЙ§AЃЈ3ЃЌ3ЃЉЃЌгыxжсе§АыжсНЛгкBЕуЃЌгыyжсНЛгкCЕуЃЌЁїABCЕФЭтНгдВЧЁКУОЙ§дЕуO.
ЕФЭМЯѓОЙ§AЃЈ3ЃЌ3ЃЉЃЌгыxжсе§АыжсНЛгкBЕуЃЌгыyжсНЛгкCЕуЃЌЁїABCЕФЭтНгдВЧЁКУОЙ§дЕуO.

ЃЈ1ЃЉЧѓBЕуЕФзјБъМАЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉХзЮяЯпЩЯвЛЕуQЃЈmЃЌm+3ЃЉЃЌЃЈmЮЊећЪ§ЃЉЃЌЕуMЮЊЁїABCЕФЭтНгдВЩЯвЛЖЏЕуЃЌЧѓЯпЖЮQMГЄЖШЕФЗЖЮЇЃЛ
ЃЈ3ЃЉНЋЁїAOCШЦЦНУцФквЛЕуPа§зЊ180ЁужСЁїA'O'C'ЃЈЕуO'гыOЮЊЖдгІЕуЃЉЃЌЪЙЕУИУШ§НЧаЮЕФЖдгІЕужаЕФСНИіЕуТфдк![]() ЕФЭМЯѓЩЯЃЌЧѓГіа§зЊжааФPЕФзјБъ.
ЕФЭМЯѓЩЯЃЌЧѓГіа§зЊжааФPЕФзјБъ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
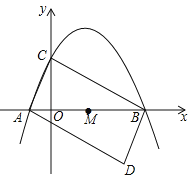
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=Љ![]() x2+
x2+![]() x+2гыxжсНЛгкЕуAЃЌBЃЌгыyжсНЛгкЕуCЃЎ
x+2гыxжсНЛгкЕуAЃЌBЃЌгыyжсНЛгкЕуCЃЎ
ЃЈ1ЃЉЪдЧѓAЃЌBЃЌCЕФзјБъЃЛ
ЃЈ2ЃЉНЋЁїABCШЦABжаЕуMа§зЊ180ЁуЃЌЕУЕНЁїBADЃЎ3
ЂйЧѓЕуDЕФзјБъЃЛ
ЂкХаЖЯЫФБпаЮADBCЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉдкИУХзЮяЯпЖдГЦжсЩЯЪЧЗёДцдкЕуPЃЌЪЙЁїBMPгыЁїBADЯрЫЦЃПШєДцдкЃЌЧыжБНгаДГіЫљгаТњзуЬѕМўЕФPЕуЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
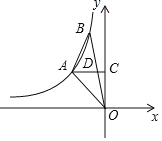
ЁОЬтФПЁПШчЭМЃЌAЁЂBЪЧЗДБШР§КЏЪ§![]() ЭМЯѓЩЯЕФСНЕуЃЌЙ§ЕуAзїACЁЭyжсЃЌДЙзуЮЊCЃЌНЛOBгкЕуDЃЌЧвDЮЊOBЕФжаЕуЃЌШєЁїABOЕФУцЛ§ЮЊ4ЃЌдђkЕФжЕЮЊ______.
ЭМЯѓЩЯЕФСНЕуЃЌЙ§ЕуAзїACЁЭyжсЃЌДЙзуЮЊCЃЌНЛOBгкЕуDЃЌЧвDЮЊOBЕФжаЕуЃЌШєЁїABOЕФУцЛ§ЮЊ4ЃЌдђkЕФжЕЮЊ______.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
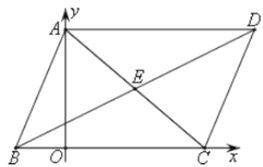
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЦНааЫФБпаЮABCDжаЖЅЕуAзјБъ(0,6)ЃЌЖЅЕуBзјБъ(-2,0)ЃЌЖЅЕуCзјБъ(8,0),ЕуEЮЊЦНааЫФБпаЮABCDЕФЖдНЧЯпЕФНЛЕуЃЌЧѓЙ§ЕуEЧвЕНЕуCЕФОрРызюДѓЕФжБЯпНтЮіЪН____.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдгкЖўДЮКЏЪ§yЃНx2Љ4x+3КЭвЛДЮКЏЪ§yЃНЉx+1ЃЌЮвУЧАбyЃНtЃЈx2Љ4x+3ЃЉ+ЃЈ1ЉtЃЉЃЈЉx+1ЃЉГЦЮЊетСНИіКЏЪ§ЕФЁАдйЩњЖўДЮКЏЪ§ЁБЃЌЦфжаtЪЧВЛЮЊСуЕФЪЕЪ§ЃЌЦфЭМЯѓМЧзїХзЮяЯпEЃЎЯжгаЕуAЃЈ1ЃЌ0ЃЉКЭХзЮяЯпEЩЯЕФЕуBЃЈ2ЃЌnЃЉЃЌЧыЭъГЩЯТСаШЮЮёЃК
ЃЈГЂЪдЃЉ
ЂХХаЖЯЕуAЪЧЗёдкХзЮяЯпEЩЯЃЛ
ЂЦЧѓnЕФжЕЃЎ
ЃЈЗЂЯжЃЉЭЈЙ§ЃЈ1ЃЉКЭЃЈ2ЃЉЕФбнЫуПЩжЊЃЌЖдгкtШЁШЮКЮВЛЮЊСуЕФЪЕЪ§ЃЌХзЮяЯпEзмЙ§ЖЈЕуЃЌЧыФуЧѓГіЖЈЕуЕФзјБъЃЎ
ЃЈгІгУЃЉЖўДЮКЏЪ§yЃНЉ3x2+8xЉ5ЪЧЖўДЮКЏЪ§yЃНx2Љ4x+3КЭвЛДЮКЏЪ§yЃНЉx+1ЕФвЛИіЁАдйЩњЖўДЮКЏЪ§ЁБТ№ЃПШчЙћЪЧЃЌЧѓГіtЕФжЕЃЛШчЙћВЛЪЧЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЭЌвЛЦНУцжБНЧзјБъЯЕжаЃЌвЛДЮКЏЪ§y=kx-2kКЭЖўДЮКЏЪ§y=-kx2+2x-4(kЪЧГЃЪ§ЧвkЁй0)ЕФЭМЯѓПЩФмЪЧ( )
A.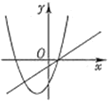 B.
B.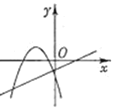
C. D.
D.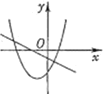
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com