
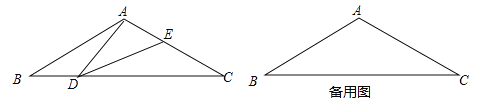
【题目】如图,在等腰三角形ABC中,∠BAC=120°,AB=AC=2,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=30°.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式并写出自变量x的取值范围.
【答案】(1)答案见解析;(2)![]() (0<x<
(0<x<![]() ).
).
【解析】试题分析:(1)根据两角相等得到△ABD∽△DCE;
(2)如图1,作高AF,根据直角三角形30°的性质求AF的长,根据勾股定理求BF的长,则可得BC的长,根据(1)中的相似列比例式可得函数关系式,并确定取值.
(1)∵△ABC是等腰三角形,且∠BAC=120°,∴∠ABD=∠ACB=30°,∴∠ABD=∠ADE=30°,∵∠ADC=∠ADE+∠EDC=∠ABD+∠DAB,∴∠EDC=∠DAB,∴△ABD∽△DCE;
(2)如图1,∵AB=AC=2,∠BAC=120°,过A作AF⊥BC于F,∴∠AFB=90°,∵AB=2,∠ABF=30°,∴AF=![]() AB=1,∴BF=
AB=1,∴BF=![]() ,∴BC=2BF=
,∴BC=2BF=![]() ,则DC=
,则DC=![]() ﹣x,EC=2﹣y,∵△ABD∽△DCE,∴
﹣x,EC=2﹣y,∵△ABD∽△DCE,∴![]() ,∴
,∴![]() ,化简得:
,化简得: ![]() (0<x<
(0<x<![]() ).
).


科目:初中数学 来源: 题型:
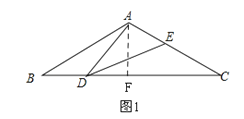
【题目】如图,在直线l上摆放着三个三角形:△ABC、△HFG、△DCE,已知BC=![]() CE,F、G分别是BC、CE的中点,FM∥AC∥HG∥DE,GN∥DC∥HF∥AB.设图中三个四边形的面积依次是S1,S2,S3,若S1+S3=20,则S1=_____,S2=_____.
CE,F、G分别是BC、CE的中点,FM∥AC∥HG∥DE,GN∥DC∥HF∥AB.设图中三个四边形的面积依次是S1,S2,S3,若S1+S3=20,则S1=_____,S2=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016·大连中考)如图,抛物线y=x2-3x+![]() 与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E.
与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E.
(1)求直线BC的解析式;
(2)当线段DE的长度最大时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
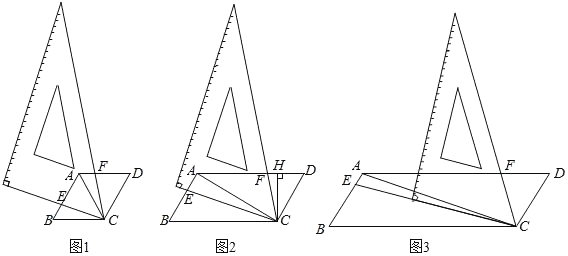
【题目】数学活动课上,某学习小组对有一内角为120°的平行四边形ABCD(∠BAD=120°)进行探究:将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB,AD于点E,F(不包括线段的端点).
(1)初步尝试
如图1,若AD=AB,试猜想线段AE、AF、AC之间的数量关系;
(2)类比发现
如图2,若AD=2AB,过点C作CH⊥AD于点H,求![]() 的值;
的值;
(3)深入探究
如图3,若AD=4AB,探究得:![]() 的值为常数t,则t= .
的值为常数t,则t= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有四个分别标有数字1,2,3,4的小球,它们的形状、大小、质地等完全相同.小米先从盒子中随机取出一个小球,记下数字为x,且不放回盒子,再由小华随机取出一个小球,记下数字为y.
(1)用列表法或画树状图表示出(x,y)的所有可能出现的结果;
(2)求小米、小华各取一次小球所确定的点(x,y)落在反比例函数y=![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
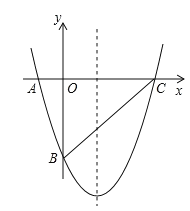
【题目】如图,已知二次函数![]() 的图象与坐标轴交于点A(-1,0)和点B(0,-5).
的图象与坐标轴交于点A(-1,0)和点B(0,-5).
(1)求该二次函数的解析式;
(2)已知该函数图象的对称轴上存在一点P,使得△ABP的周长最小,请求出点P的坐标;
(3)设二次函数![]() 的图象与x轴的另一交点为点C,连接BC,点N是线段BC上一点,过点N作y轴的平行线交抛物线于点M,求当四边形OBMN为平行四边形时,点N的坐标.
的图象与x轴的另一交点为点C,连接BC,点N是线段BC上一点,过点N作y轴的平行线交抛物线于点M,求当四边形OBMN为平行四边形时,点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
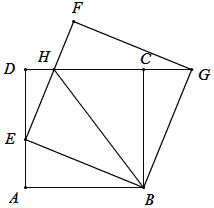
【题目】如图,正方形ABCD的边长为2,点E是AD边上的动点,从点A开始沿AD向D运动.以BE为边,在BE的上方作正方形BEFG,EF交DC于点H,连接CG、BH.请探究:
(1)线段AE与CG是否相等?请说明理由.
(2)若设AE=x,DH=y,当x取何值时,y最大?最大值是多少?
(3)当点E运动到AD的何位置时,△BEH∽△BAE?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题,探究函数y=x2﹣2![]() 的图象与性质,小张根据学习函数的经验,对函数y=x2﹣2
的图象与性质,小张根据学习函数的经验,对函数y=x2﹣2![]() 的图象与性质进行了研究,下面是小张的探究过程,请补充完整:
的图象与性质进行了研究,下面是小张的探究过程,请补充完整:
(1)函数y=x2﹣2![]() 的自变量取值范围是 .
的自变量取值范围是 .
(2)下表是y与x的几组对应值:
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | |
y | … | n | 3 | 0 | ﹣1 | 0 | ﹣1 | 0 | 3 | m |
求m的值;
(3)如图,在平面直角坐标系xOy中,算出了以上表中各对对应值为坐标的点,根据算出的点,画出该函数的图象;
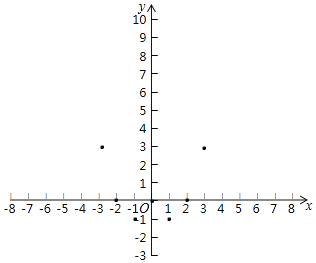
(4)进一步探究发现,该函数图象在第四象限内的最低点是1,﹣1),结合函数的图象,写出该函数的其他性质(一条即可);
(5)根据图象回答:方程x2﹣2![]() =﹣
=﹣![]() 有 个实数解.
有 个实数解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题发现
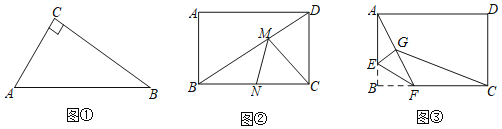
(1)如图①,Rt△ABC中,∠C=90°,AC=6,BC=8,点D是AB边上任意一点,则CD的最小值为 ;
(2)如图②,矩形ABCD中,AB=6,BC=8,点M、点N分别在ED、BC上,求CM+MN的最小值;
(3)如图③.矩形ABCD中,AB=6,BC=8,点E是AB边上一点,且AE=4,点F是EC边上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG、CG,四边形AGCD的面积是否存在最小值,若在在,求这个最小值及此时BF的长度.若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com