
【题目】有这样一个问题,探究函数y=x2﹣2![]() 的图象与性质,小张根据学习函数的经验,对函数y=x2﹣2
的图象与性质,小张根据学习函数的经验,对函数y=x2﹣2![]() 的图象与性质进行了研究,下面是小张的探究过程,请补充完整:
的图象与性质进行了研究,下面是小张的探究过程,请补充完整:
(1)函数y=x2﹣2![]() 的自变量取值范围是 .
的自变量取值范围是 .
(2)下表是y与x的几组对应值:
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | |
y | … | n | 3 | 0 | ﹣1 | 0 | ﹣1 | 0 | 3 | m |
求m的值;
(3)如图,在平面直角坐标系xOy中,算出了以上表中各对对应值为坐标的点,根据算出的点,画出该函数的图象;
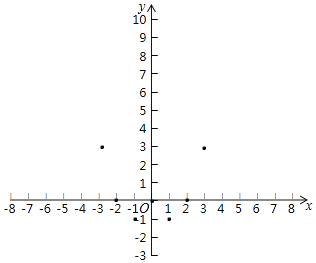
(4)进一步探究发现,该函数图象在第四象限内的最低点是1,﹣1),结合函数的图象,写出该函数的其他性质(一条即可);
(5)根据图象回答:方程x2﹣2![]() =﹣
=﹣![]() 有 个实数解.
有 个实数解.
【答案】(1)自变量取值范围是任意实数;(2)m的值为8;(3)如图见解析;(4)当x<﹣1时,y随x的增大而减小.(5)方程x2﹣2![]() =﹣
=﹣![]() 有3个实数解.
有3个实数解.
【解析】
(1)根据二次根式的意义和函数关系式即可求解;
(2)根据函数关系式将x的值代入即可求解;
(3)根据表格数据,描点,连线,即可画出图象;
(4)观察函数图像,利用增减性写出一条性质;
(5)根据图象将y=x2-2![]() 的图象向下平移0.5个单位长度与原函数图象有三个交点即可求解.
的图象向下平移0.5个单位长度与原函数图象有三个交点即可求解.
(1)根据函数解析式可知:无论x为何值,![]() 均有意义,
均有意义,
∴自变量取值范围是任意实数.
故答案为任意实数.
(2)当x=4时,y=![]() .
.
答:m的值为8.
(3)如图:
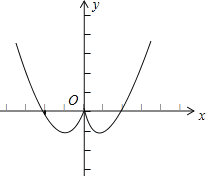
(4)根据函数图象可知:
当x<﹣1时,y随x的增大而减小.
(5)根据图象可知:
直线y=﹣![]() ,与函数图象有三个交点,即可得:
,与函数图象有三个交点,即可得:
方程x2﹣2![]() =﹣
=﹣![]() 有3个实数解.
有3个实数解.


科目:初中数学 来源: 题型:
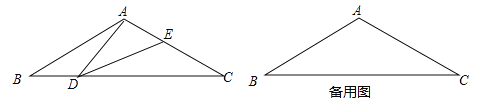
【题目】如图,在等腰三角形ABC中,∠BAC=120°,AB=AC=2,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=30°.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式并写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实素质教育要求,促进学生全面发展,我市某中学2016年投资11万元新增一批电脑,计划以后每年以相同的增长率进行投资,2018年投资18.59万元.
(1)求该学校为新增电脑投资的年平均增长率;
(2)从2016年到2018年,该中学三年为新增电脑共投资多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据《北京晚报》介绍,自2009年故宫博物院年度接待观众首次突破1000万人次之后,每年接待量持续增长,到2018年突破1700万人次,成为世界上接待量最多的博物馆.特别是随着《我在故宫修文物》、《上新了,故宫》等一批电视文博节目的播出,社会上再次掀起故宫热.于是故宫文创营销人员为开发针对不同年龄群体的文创产品,随机调查了部分参观故宫的观众的年龄,整理并绘制了如下统计图表.
2018年参观故宫观众年龄频数分布表
年龄x/岁 | 频数/人数 | 频率 |
20≤x<30 | 80 | b |
30≤x<40 | a | 0.240 |
40≤x<50 | 35 | 0.175 |
50≤x<60 | 37 | c |
合计 | 200 | 1.000 |
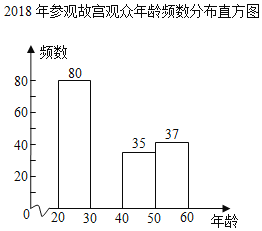
(1)求表中a,b,c的值;
(2)补全频数分布直方图;
(3)从数据上看,年轻观众(20≤x<40)已经成为参观故宫的主要群体.如果今年参观故宫人数达到2000万人次,那么其中年轻观众预计约有 万人次.
查看答案和解析>>
科目:初中数学 来源: 题型:
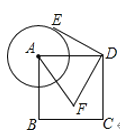
【题目】如图,已知正方形ABCD的边长为4,以点A为圆心,2为半径作圆,点E是⊙A上的任意一点,将点E绕点D按逆时针方向转转90°得到点F,连接AF、DF,则![]() 的最小值是__.
的最小值是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是等边△ABC边AB上的一点,且AD:DB=1:2,现将△ABC折叠,使点C与D重合,折痕为EF,点E、F分别在AC和BC上,则CE:CF的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,二次函数![]() 的图象经过A(3,3),与x轴正半轴交于B点,与y轴交于C点,△ABC的外接圆恰好经过原点O.
的图象经过A(3,3),与x轴正半轴交于B点,与y轴交于C点,△ABC的外接圆恰好经过原点O.

(1)求B点的坐标及二次函数的解析式;
(2)抛物线上一点Q(m,m+3),(m为整数),点M为△ABC的外接圆上一动点,求线段QM长度的范围;
(3)将△AOC绕平面内一点P旋转180°至△A'O'C'(点O'与O为对应点),使得该三角形的对应点中的两个点落在![]() 的图象上,求出旋转中心P的坐标.
的图象上,求出旋转中心P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=x2﹣4x+3和一次函数y=﹣x+1,我们把y=t(x2﹣4x+3)+(1﹣t)(﹣x+1)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线E.现有点A(1,0)和抛物线E上的点B(2,n),请完成下列任务:
(尝试)
⑴判断点A是否在抛物线E上;
⑵求n的值.
(发现)通过(1)和(2)的演算可知,对于t取任何不为零的实数,抛物线E总过定点,请你求出定点的坐标.
(应用)二次函数y=﹣3x2+8x﹣5是二次函数y=x2﹣4x+3和一次函数y=﹣x+1的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com