
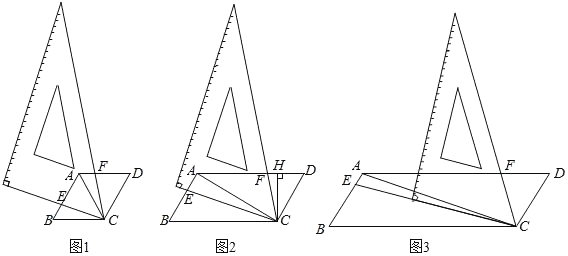
【题目】数学活动课上,某学习小组对有一内角为120°的平行四边形ABCD(∠BAD=120°)进行探究:将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB,AD于点E,F(不包括线段的端点).
(1)初步尝试
如图1,若AD=AB,试猜想线段AE、AF、AC之间的数量关系;
(2)类比发现
如图2,若AD=2AB,过点C作CH⊥AD于点H,求![]() 的值;
的值;
(3)深入探究
如图3,若AD=4AB,探究得:![]() 的值为常数t,则t= .
的值为常数t,则t= .
【答案】(1)AE+AF=AC;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)先证明△ABC,△ACD都是等边三角形,再证明∠BCE=∠ACF,从而可证得△BCE≌△ACF,进而证得BE=AF,由此即可解决问题.
(2)设DH=x,由题意,CD=2x,CH=![]() ,由△ACE∽△HCF,得
,由△ACE∽△HCF,得![]() ,由此即可得出答案.
,由此即可得出答案.
(3)作CN⊥AD于N,CM⊥BA于M,CM与AD交于点H.先证明△CFN∽△CEM,得![]() ,由ABCM=ADCN,AD=4AB,推出CM=4CN,所以
,由ABCM=ADCN,AD=4AB,推出CM=4CN,所以![]() ,设CN=a,FN=b,则CM=4a,EM=4b,想办法求出AC,AE+4AF即可解决问题.
,设CN=a,FN=b,则CM=4a,EM=4b,想办法求出AC,AE+4AF即可解决问题.
解:(1)AE+AF=AC; 理由如下:
∵四边形ABCD是平行四边形,∠BAD=120°,
∴∠D=∠B=60°,
∵四边形ABCD是菱形,
∴AD=AB,
∴△ABC,△ACD都是等边三角形,
∴∠B=∠CAD=60°,∠ACB=60°,BC=AC,
∵∠ECF=60°,
∴∠BCE+∠ACE=∠ACF+∠ACE=60°,
∴∠BCE=∠ACF,
在△BCE和△ACF中, ,
,
∴△BCE≌△ACF(ASA).
∴BE=AF,
∴AE+AF=AE+BE=AB=AC;
故答案为:AE+AF=AC;
(2)设DH=x,由由题意,CD=2x,CH=![]() ,
,
∴AD=2AB=4x,
∴AH=AD﹣DH=3x,
∵CH⊥AD,
∴AC=![]() =
=![]() ,
,
∴AC2+CD2=AD2,
∴∠ACD=90°,
∴∠BAC=∠ACD=90°,
∴∠CAD=30°,
∴∠ACH=60°,
∵∠ECF=60°,
∴∠HCF=∠ACE,
∴△ACE∽△HCF,
∴![]() ,
,
(3)![]() ,
,
理由如下:
如图,作CN⊥AD于N,CM⊥BA于M,CM与AD交于点H.

∵∠ECF+∠EAF=180°,
∴∠AEC+∠AFC=180°,
∵∠AFC+∠CFN=180°,
∴∠CFN=∠AEC,∵∠M=∠CNF=90°,
∴△CFN∽△CEM,
∴![]() ,
,
∵ABCM=ADCN,AD=4AB,
∴CM=4CN,
∴![]() ,
,
设CN=a,FN=b,则CM=4a,EM=4b,
∵∠MAH=60°,∠M=90°,
∴∠AHM=∠CHN=30°,
∴HC=2a,HM=2a,HN=![]() a,
a,
∴AM=![]() ,AH=
,AH=![]() ,
,
∴AC=![]() =
=![]() ,
,
AE+4AF=(EM﹣AM)+4(AH+HN﹣FN)=EM﹣AM+4AH+4HN﹣4FN=4AH+4HN﹣AM=![]() ,
,
∴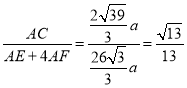 .
.
∴t=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
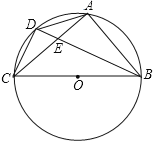
【题目】如图,⊙O是△ABC的外接圆,BC是⊙O的直径,D是劣弧![]() 的中点BD交AC于点E.
的中点BD交AC于点E.
(1)求证:AD2=DEDB.
(2)若BC=5,CD=![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于![]() 的一元二次方程
的一元二次方程![]() 有两个实数根,且其中一个根为另一个根的
有两个实数根,且其中一个根为另一个根的![]() 倍,那么称这样的方程为“倍根方程”,例如,一元二次方程
倍,那么称这样的方程为“倍根方程”,例如,一元二次方程![]() 的两个根是
的两个根是![]() 和
和![]() ,则方程
,则方程![]() 就是“倍根方程”.
就是“倍根方程”.
(1)若一元二次方程![]() 是“倍根方程”,则
是“倍根方程”,则![]() = .
= .
(2)若关于![]() 的一元二次方程
的一元二次方程![]() 是“倍根方程”,则
是“倍根方程”,则![]() ,
,![]() ,
,![]() 之间的关系为 .
之间的关系为 .
(3)若![]() 是“倍根方程”,求代数式
是“倍根方程”,求代数式![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
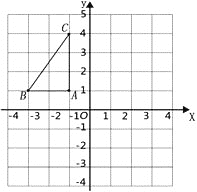
【题目】如图,在平面直角坐标系中,已知 ![]() ABC的三个顶点的坐标分别为A(-1,1), B(-3,1),C(-1,4).
ABC的三个顶点的坐标分别为A(-1,1), B(-3,1),C(-1,4).
①画出△ABC关于y轴对称的△A1B1C1;
②将△ABC绕着点B顺时针旋转90°后得到△A2BC2 , 请在图中画出△A2BC2 , 并求出线段BC旋转过程中所扫过的面积(结果保留 ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
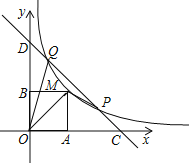
【题目】如图,在平面直角坐标系xOy中,函数y=![]() (m为常数,m>1,x>0)的图象经过点P(m,1)和Q(1,m),直线PQ与x轴,y轴分别交于C,D两点,点M(x,y)是该函数图象上的一个动点,过点M分别作x轴和y轴的垂线,垂足分别为A,B.
(m为常数,m>1,x>0)的图象经过点P(m,1)和Q(1,m),直线PQ与x轴,y轴分别交于C,D两点,点M(x,y)是该函数图象上的一个动点,过点M分别作x轴和y轴的垂线,垂足分别为A,B.
(1)求∠OCD的度数;
(2)当m=3,1<x<3时,存在点M使得△OPM∽△OCP,求此时点M的坐标;
(3)当m=5时,矩形OAMB与△OPQ的重叠部分的面积能否等于4.1?请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
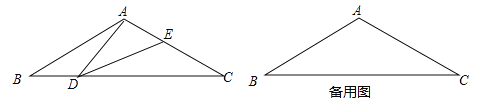
【题目】如图,在等腰三角形ABC中,∠BAC=120°,AB=AC=2,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=30°.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式并写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实素质教育要求,促进学生全面发展,我市某中学2016年投资11万元新增一批电脑,计划以后每年以相同的增长率进行投资,2018年投资18.59万元.
(1)求该学校为新增电脑投资的年平均增长率;
(2)从2016年到2018年,该中学三年为新增电脑共投资多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,二次函数![]() 的图象经过A(3,3),与x轴正半轴交于B点,与y轴交于C点,△ABC的外接圆恰好经过原点O.
的图象经过A(3,3),与x轴正半轴交于B点,与y轴交于C点,△ABC的外接圆恰好经过原点O.

(1)求B点的坐标及二次函数的解析式;
(2)抛物线上一点Q(m,m+3),(m为整数),点M为△ABC的外接圆上一动点,求线段QM长度的范围;
(3)将△AOC绕平面内一点P旋转180°至△A'O'C'(点O'与O为对应点),使得该三角形的对应点中的两个点落在![]() 的图象上,求出旋转中心P的坐标.
的图象上,求出旋转中心P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com