Question

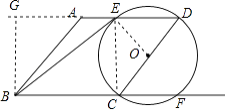
【题目】如图，在菱形ABCD中，AB=4，取CD中点O，以O为圆心OD为半径作圆交AD于E，交BC的延长线交于点F，
（1）若cos∠AEB= ，则菱形ABCD的面积为；
（2）当BE与⊙O相切时，AE的长为 ．

Answer 1

【答案】
（1）8
（2）6﹣2
【解析】解：（1.）作BG⊥AD于G，连接CE，
∵四边形ABCD是菱形∴AB=AD=BC=CD=4，AD∥BC，∵CD是直径，∴∠CED=90°，∴CE⊥AD，∴BG∥CE，∴四边形BCEG是矩形，∴GE=BC=4，∵cos∠AEB= ，∴ = ，∴BE= ×4=6，∴BG= = =2 ，∴菱形ABCD的面积=ADBG=4×2 =8 ；
所以答案是8 ；
（2.）连接OE，∵BE与⊙O相切，∴FE⊥BE，∴∠BEG=∠CEO，∵OE=OC，∴∠DCE=∠CEO，∴∠ECD=∠GEB，∴ = ，∵GE=AD，∴AG=ED，设BG=CE=a，∴ = ，∴16﹣a2=4AE，∴AG2=4AE，即（4﹣AE）2=4AE，∴AE2﹣12AE+16=0，解得AE=6﹣2 或AE=6+2 （不合题意，舍去），所以答案是6﹣2 ．

【考点精析】利用菱形的性质和切线的性质定理对题目进行判断即可得到答案，需要熟知菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半；切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径．