
����Ŀ����֪����Rt��ABC�͵���Rt��AED�У���ACB=��AED=90������AD=AC��
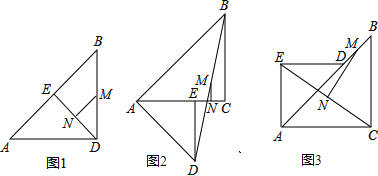
��1�����֣���ͼ1������E��AB���ҵ�C�͵�D�غ�ʱ������M��N�ֱ���DB��EC���е㣬��MN��EC��λ�ù�ϵ�� ��MN��EC��������ϵ�� ��
��2��̽�������ѣ�1��С���е���AED�Ƶ�A˳ʱ����ת45���õ���ͼ2������BD��EC��������DB��EC���е�M��N����MN��EC��λ�ù�ϵ��������ϵ��Ȼ�ܳ������������������֤����������������˵�����ɣ�
��3�����ѣ�1��С���е���AED�Ƶ�A��ʱ����ת45���õ���ͼ3������BD��EC��������DB��EC���е�M��N����MN��EC��λ�ù�ϵ��������ϵ��Ȼ�ܳ������������������֤����������������˵�����ɣ�
���𰸡���1��MN��EC��MN=![]() EC����2�����������ɼ���������3�����������ɼ�����
EC����2�����������ɼ���������3�����������ɼ�����
��������
�����������1��������λ�߶�������ϵ���ֱ�����������ʼ���ֱ�ӵó����ۣ�
��2������EM���ӳ���BC��F��֤����EDM�ա�FBM�������߶εĵ�������������⣻
��3���ӳ�ED��BC�ڵ�F������AF��MF����Ͼ��ε����ʺ͵���ֱ�����������ʣ��������ýǵĵ�������������⣮
�⣺��1��MN��EC��MN=![]() EC��
EC��
�ɵ���Rt��ABC�͵���Rt��AED�У���ACB=��AED=90����
��֪��AE=BE=EC��DE��AB��
����M��N�ֱ���DB��EC���е㣬
��MN��AB����MN=![]() BE��
BE��
��MN��EC��MN=![]() EC��
EC��
��2����ͼ2
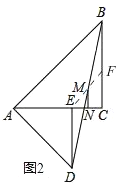
����EM���ӳ���BC��F��
�ߡ�AED=��ACB=90����
��DE��BC��
���DEM=��AFM����EDM=��MBF��
��BM=MD��
����EDM����FBM��
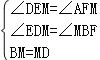 ��
��
���EDM�ա�FBM��
��BF=DE=AE��EM=FM��
��MN=![]() FC=
FC=![]() ��BC��BF��=
��BC��BF��=![]() ��AC��AF��=
��AC��AF��=![]() EC��
EC��
��MN��EC��
��3����ͼ3
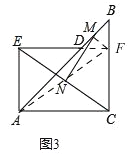
�ӳ�ED��BC�ڵ�F������AF��MF����AFΪ����ACFE�Խ��ߣ����Աؾ���EC���е�N��AN=NF=EN=NC��
��Rt��BDF�У�M��BD���е㣬��B=45����
��FD=FB��
��FM��AB��
��MN=NA=NF=NC��
��MN=![]() EC��
EC��
���NAM=��AMN����NAC=��NCA��
���MNF=��NAM+��AMN=2��NAM����FNC=��NAC+��NCA=2��NAC��
���MNC=��MNF+��FNC=2��NAM+2��NAC=2����NAM+��NAC��=2��DAC=90����
���MNC=90����
��MN��FC��MN=![]() EC��
EC��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��n+1���߳�Ϊ2�ĵȱ���������һ������ͬһֱ���ϣ����B2D1C1�����ΪS1 �� ��B3D2C2�����ΪS2 �� ������Bn+1DnCn�����ΪSn �� ��Sn=���ú�n��ʽ�ӱ�ʾ���� 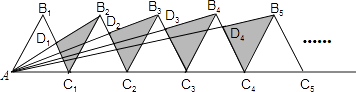
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ϵxOy�У�A����4��0����B��0��2��������AB���ӳ���C������CO������COB�ס�CAO�����C������Ϊ�� �� 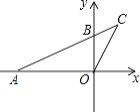
A.��1�� ![]() ��
��
B.�� ![]() ��
�� ![]() ��
��
C.�� ![]() ��2
��2 ![]() ��
��
D.�� ![]() ��2
��2 ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�����߳�Ϊa��b��c�����������ܹ�˵����ABC��ֱ�������ε��ǣ� ��
A. a��b��c��5��12��15 B. 3a=4b=5c C. a��b��c��1��2��![]() D. a=b=
D. a=b=![]() c
c
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ı���ABCD��ƽ���ı��Σ�BC=3AB��A��B���������ֱ��ǣ���1��0������0��2����C��D�����ڷ���������y= ![]() ��x��0����ͼ���ϣ���k��ֵ���� ��
��x��0����ͼ���ϣ���k��ֵ���� �� 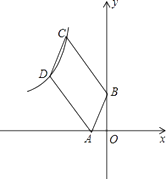
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
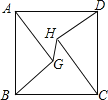
����Ŀ����ͼ������ABCD�߳�Ϊ10��AG=CH=8��BG=DH=6������GH�����߶�GH�ij�Ϊ��������
A. ![]() B.
B. ![]() C.
C. ![]() D. 10-5
D. 10-5![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��ͼ1����M��N���߶�AB�ָ��AM��MN��BN������AM��MN��BNΪ�ߵ���������һ��ֱ�������Σ���Ƶ�M��N���߶�AB�Ĺ��ɷָ��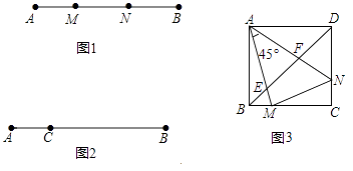
��1����֪��M��N���߶�AB�Ĺ��ɷָ�㣬��AM=3��MN=4��BN�ij���
��2����֪��C���߶�AB�ϵ�һ���㣬��λ����ͼ2��ʾ������BC�ϻ�һ��D��ʹC��D���߶�AB�Ĺ��ɷָ�㣨Ҫ��߹���ͼ��������ͼ�ۼ�������һ�����μ��ɣ�
��3����ͼ3��������ABCD�У�M��N�ֱ���BC��DC�ϣ���BM��DN����MAN=45�㣬AM��AN�ֱ�BD��E��F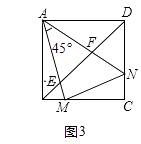
��֤����E��F���߶�BD�Ĺ��ɷָ�㣻
�ڡ�AMN������ǡ�AEF�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ������˵��������ǣ������� 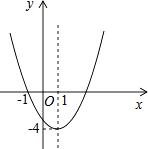
A.ͼ�����ֱ��x=1�Գ�
B.����y=ax2+bx+c��a��0������Сֵ�ǩ�4
C.��1��3�Ƿ���ax2+bx+c=0��a��0����������
D.��x��1ʱ��y��x�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABC�������������ֱ�ΪA��0��3����B����3��5����C����4��1����
�ٰѡ�ABC����ƽ��2����λ�á�A1B1C1 �� �뻭����A1B1C1 �� ��д����A1�����ꣻ
�ڰѡ�ABC��ԭ��O��ת180��õ���A2B2C2 �� �뻭����A2B2C2 ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com