
����Ŀ�� ��ѧϰ��ȫ�������κ͵ȱ������ε�֪ʶ��������ʦ��������һ��������ͼ����B���߶�AC������һ�����ֱ���AB��BCΪ����ACͬһ�����ȱߡ�ABD�͵ȱߡ�BCE������CD��AE�ֱ���BE��DB���ڵ�N��M������MN��
(1)��֤����ABE�ա�DBC��

��������ʦ����ѧ����С�����̽�����㻹�ܵó�ʲô���ۣ�
��ӢС��̽���Ľ�������AM=DN��
�ܶ�С��̽���Ľ���������EMB�ա�CNB��
����С��̽���Ľ�������MN��AC��
��2������Ϊ��һС��̽���Ľ�������ȷ�ģ�
��3��ѡ����������Ϊ��ȷ��һ�����μ���֤����
���𰸡���1��֤������������2������С��̽���Ľ��۶���ȷ����3��֤��������
�����������������
��1���ɡ�ABD�͡�BCE���ǵȱ������οɵã�AB=DB��BC=BE����ABD=��EBC=60���������ɵ���ABE=��DBC���Ӷ����ɡ�SAS��֤����ABE�ա�DBC��
��2������ABE�ա�DBC�ɵ���EAB=��CDB��������֪������֤��DBN=��ABD=60�������AB=DB��֤��ABM�ա�DBN���Ϳɵ�AM=DN��ͬ����֤��EBM�ա�CBN������EBM�ա�CBN�ɵ�BM=BN����ϡ�DBN=60���ɵá�BMN�ǵȱ������Σ��Ӷ��ɵá�MNB=60��=��EBC���ɴ˿ɵ�MN��AC��������С���̽�����۶�����ȷ�ģ�
��3�����ݣ�2���еķ���ѡ���һ������֤�����ɣ�
���������
��1�ߡ�ABD����BCE���ǵȱ���������
��AB=DB��BE=BC����ABD=��EBC=60����
���ABE=��DBC=120�㣬
���ڡ�ABE�͡�DBC�У�AB=DB����ABE=��DBC��BE=BC��
���ABE�ա�DBC��
��2������С��̽���Ľ��۶���ȷ��
��3��ѡ��֤����AM=DN���������£�
�ߡ�ABE�ա�DBC��
����EAB=��CDB��
�ߡ�ABD+��DBE+��EBC=180������ABD=��EBC=60����
���DBE=��ABD=60����
���ڡ�ABM�͡�DBN�У���MAB=��NDB��AB=DB����DBN=��ABM��
���ABM�ա�DBN��
��AM=DN.


 ǧ�������������ĩ�����Ծ�����ϵ�д�
ǧ�������������ĩ�����Ծ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
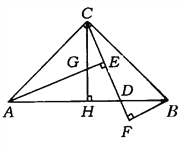
����Ŀ����ͼ���ڵ���Rt��ABC�У���C��90�㣬D��б����AB����һ�㣬AE��CD��E��BF��CD��CD���ӳ�����F��CH��AB��H�㣬��AE��G��
��1����˵��AH��BH
��2����֤��BD��CG��
��3��̽��AE��EF��BF֮���������ϵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A��2x��4��x��2�����������ϣ���x��ֵ���ڣ� ��
A. 2 B. ��2 C. 2��2 D. ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�������
�У�������![]() �ĶԳ�����ֱ��
�ĶԳ�����ֱ��![]() ��
��
��1���������ߵı���ʽ��
��2����![]() ��
�� ![]() ���������ϣ���
���������ϣ���![]() ����ֱ��д��
����ֱ��д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3�����![]() Ϊ�������ϵ�һ�����㣬��
Ϊ�������ϵ�һ�����㣬��![]() ʱ����
ʱ����![]() ����
����![]() ��ĶԳƵ㶼��ֱ��
��ĶԳƵ㶼��ֱ��![]() ���Ϸ�����
���Ϸ�����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ACD�ǡ�ABC��һ�������CA=CB��
��1��������ACD�Ľ�ƽ����CE��
��2����֤��CE��AB��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����|x|=3��|y|=4����|x��y|=y��x����xy��ֵΪ�� ��
A.��1
B.��12
C.12
D.12��12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
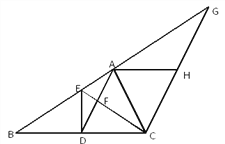
����Ŀ������ABC�У�D��BC���е㣬��AD��AC��DE��BC����AB�ཻ�ڵ�E��EC��AD�ཻ�ڵ�F����C����CG��AD����BA���ӳ�����G����A��BC��ƽ���߽�CG��H����
��1������BAC��900����֤���ı���ADCH�����Σ�
��2����֤����ABC�ס�FCD��
��3����DE��3��BC��8������FCD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������֪��������Ψһ������ABC���ǣ� ��
A.AB��6��BC��3��AC��9B.AB��5��BC��4����A��30��
C.��C��90�㣬AB��6D.��A��60�㣬��B��45�㣬AB��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ݱ������һԪ���η���x2+2x��4=0��һ����ķ�Χ�ڣ� ��
x | ��1 | 0 | 1 | 2 | 3 |
x2+2x��4 | ��5 | ��4 | ��1 | 4 | 11 |
A.��1��x��0
B.0��x��1
C.1��x��2
D.2��x��3
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com