
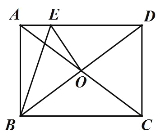
【题目】如图,矩形 ABCD 的对角线 AC 与 BD 交于点 O,点 E 在 AD 上,且 DE=CD,连接 OE,BE, ABE ![]() ACB ,若 AE=2,则 OE 的长为___________.
ACB ,若 AE=2,则 OE 的长为___________.
【答案】![]()
【解析】
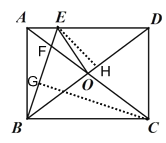
作∠ACB的平分线CG交BE于G,AC与BE交于点F,首先证明CB=CF,AF=AE=2,然后在Rt△ABC中利用勾股定理构建方程求出DE=CD=AB=6,BC=CF=AD=8,BD=AC=10,过点E作EH⊥BD于H,证明△EHD∽△BAD,利用相似三角形的性质求出EH和DH,进而可得OH,再利用勾股定理求OE即可.
解:作∠ACB的平分线CG交BE于G,AC与BE交于点F,
∵ABE=![]() ACB,GCB=
ACB,GCB=![]() ACB,
ACB,
∴ABE=GCB,
∵ABE+∠EBC=90°,
∴GCB+∠GBC=90°,
∴CG⊥BE,
∵CG平分∠ACB,
∴CB=CF,
∴∠FBC=∠BFC=∠AFE,
∵AD∥BC,
∴∠AEF=∠FBC,
∴∠AEF=∠AFE,
∴AF=AE=2,
设DE=CD=AB=x,则BC=CF=AD=x+2,AC=x+2+2=x+4,
在Rt△ABC中,AB2+BC2=AC2,即x2+(x+2)2=(x+4)2,
解得:x=6(负值已舍去),
∴DE=CD=AB=6,BC=CF=AD=8,BD=AC=10,
过点E作EH⊥BD于H,
∵∠EHD=∠BAD,∠EDH=∠BDA,
∴△EHD∽△BAD,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,![]() ,
,
∴OH=OD-DH=![]() BD-DH=
BD-DH=![]() ,
,
∴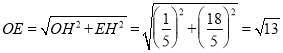 ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】观察下列两个等式:2﹣![]() =2×
=2×![]() +1,5﹣
+1,5﹣![]() =5×
=5×![]() +1,给出定义如下
+1,给出定义如下
我们称使等式a﹣b=ab+1成立的一对有理数“a,b”为共生有理数对”,记为(a,b)
(1)通过计算判断数对“﹣2,1”,“4,![]() ”是不是“共生有理数对”;
”是不是“共生有理数对”;
(2)若(6,a)是“共生有理数对”,求a的值;
(3)若(m,n)是“共生有理数对”,则“﹣n,﹣m” “共生有理数对”(填“是”或“不是”),并说明理由;
(4)若(m,n)是“共生有理数对”(其中n≠1),直接用含n的代数式表示m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情之下,中华儿女共抗时艰.重庆和湖北同饮长江水,为更好地驰援武汉,打赢防疫攻坚战,我市某公益组织收集社会捐献物资.甲、乙两人先后从![]() 地沿相同路线出发徒步前往
地沿相同路线出发徒步前往![]() 地进行物资捐献,甲出发1分钟后乙再出发,一段时间后乙追上甲,这时甲发现有东西落在
地进行物资捐献,甲出发1分钟后乙再出发,一段时间后乙追上甲,这时甲发现有东西落在![]() 地,于是原路原速返回
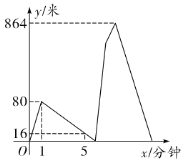
地,于是原路原速返回![]() 地去取(甲取东西的时间忽略不计),而乙继续前行,甲乙两人到达B地后原地帮忙.已知在整个过程中,甲乙均保持各自的速度匀速行走,甲、乙两人相距的路程
地去取(甲取东西的时间忽略不计),而乙继续前行,甲乙两人到达B地后原地帮忙.已知在整个过程中,甲乙均保持各自的速度匀速行走,甲、乙两人相距的路程![]() (米)与甲出发的时间
(米)与甲出发的时间![]() (分钟)之间的函数关系如图所示,则当乙到达
(分钟)之间的函数关系如图所示,则当乙到达![]() 地时,甲距
地时,甲距![]() 地的路程是_______米.
地的路程是_______米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 后得到
后得到![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后得到线段
后得到线段![]() ,分別以
,分別以![]() 、
、![]() 为圆心,
为圆心,![]() 、
、![]() 长为半径画弧
长为半径画弧![]() 和弧
和弧![]() ,连接
,连接![]() ,则图中阴影部分的面积是________.
,则图中阴影部分的面积是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC 内接于⊙O,过点 A 作⊙O 的切线交 CB 的延长线于点 P,且∠PAB=45°.
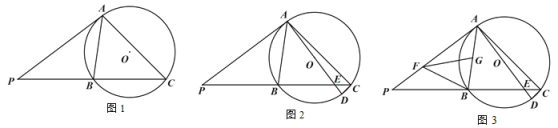
(1)如图 1,求∠ACB 的度数;
(2)如图 2,AD 是⊙O 的直径,AD 交 BC 于点 E,连接 CD,求证:AC CD ![]() ;
;
(3)如图 3 ,在(2)的条件下,当 BC 4![]() CD 时,点 F,G 分别在 AP,AB 上,连接 BF,FG,∠BFG=∠P,且 BF=FG,若 AE=15,求 FG 的长.
CD 时,点 F,G 分别在 AP,AB 上,连接 BF,FG,∠BFG=∠P,且 BF=FG,若 AE=15,求 FG 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技的进步和网络资源的丰富,在线学习已经成为更多人的自主学习选择.某校计划为学生提供以下四类在线学习方式:在线阅读、在线听课、在线答题和在线讨论.为了解学生需求,该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据调查结果绘制成如下两幅不完整的统计图.
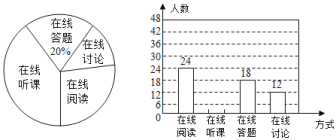
(1)求本次调查的学生总人数,并补全条形统计图;
(2)求扇形统计图中“在线讨论”对应的扇形圆心角的度数;
(3)该校共有学生2100人,请你估计该校对在线阅读最感兴趣的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年4月23日是世界读书日,某校为了解学生课外阅读情况,随机抽取![]() 名学生,对每人每周用于课外阅读的平均时间(单位:
名学生,对每人每周用于课外阅读的平均时间(单位:![]() )进行调查,过程如下:
)进行调查,过程如下:
收集数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
整理数据:
课外阅读平均时间 |
|
|
|
|
等级 |
|
|
|
|
人数 |
|
|
|
|
分析数据:
平均数 | 中位数 | 众数 |
|
|
|
请根据以上提供的信息,解答下列问题:
(1)填空:![]() ;
;![]() ;
;![]() ;
;![]() ;
;
(2)已知该校学生![]() 人,若每人每周用于课外阅读的平均时间不少于
人,若每人每周用于课外阅读的平均时间不少于![]() 为达标,请估计达标的学生数;
为达标,请估计达标的学生数;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com