
【题目】已知:△ABC 内接于⊙O,过点 A 作⊙O 的切线交 CB 的延长线于点 P,且∠PAB=45°.
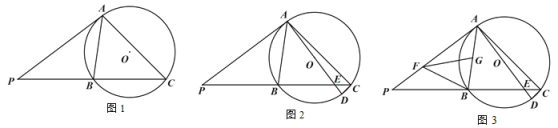
(1)如图 1,求∠ACB 的度数;
(2)如图 2,AD 是⊙O 的直径,AD 交 BC 于点 E,连接 CD,求证:AC CD ![]() ;
;
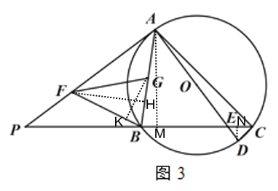
(3)如图 3 ,在(2)的条件下,当 BC 4![]() CD 时,点 F,G 分别在 AP,AB 上,连接 BF,FG,∠BFG=∠P,且 BF=FG,若 AE=15,求 FG 的长.
CD 时,点 F,G 分别在 AP,AB 上,连接 BF,FG,∠BFG=∠P,且 BF=FG,若 AE=15,求 FG 的长.
【答案】(1)∠ACB=45°;(2)见解析;(3)![]()
【解析】
(1)连接OA,OB,根据切线的性质求出∠OAB=∠OBA=45°,得到∠AOB=90°,再根据圆周角定理可得答案;
(2)作AM⊥BC于M,DN⊥BC于N,连接BD,易求![]() ,
,![]() ,然后证明△ABM≌△BDN,得到AM=BN,等量代换即可得证;
,然后证明△ABM≌△BDN,得到AM=BN,等量代换即可得证;
(3)根据(2)中结论求出![]() ,然后证明△AMC∽△DNC,AM∥DN,根据相似三角形的性质和平行线分线段成比例定理求得DE和AD,进而利用勾股定理求出CD,AC,然后即可求出AB的长,再证明△PAB∽△PCA,求出PA,可得
,然后证明△AMC∽△DNC,AM∥DN,根据相似三角形的性质和平行线分线段成比例定理求得DE和AD,进而利用勾股定理求出CD,AC,然后即可求出AB的长,再证明△PAB∽△PCA,求出PA,可得![]() ,过点G作GK⊥FB,过点F作FH⊥BG,设GK=3b,利用三角函数及等腰三角形的性质求出AH和BH,然后列方程求出b值即可解决问题.
,过点G作GK⊥FB,过点F作FH⊥BG,设GK=3b,利用三角函数及等腰三角形的性质求出AH和BH,然后列方程求出b值即可解决问题.
解:(1)连接OA,OB,则OA=OB,
∴∠OAB=∠OBA,
∵PA是⊙O的切线,
∴∠PAO=90°,
∵∠PAB=45°,
∴∠OAB=∠OBA=45°,
∴∠AOB=90°,
∴∠ACB=![]() ∠AOB=45°;
∠AOB=45°;
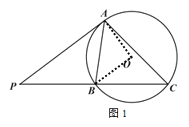
(2)作AM⊥BC于M,DN⊥BC于N,连接BD,
∵AD是⊙O的直径,
∴∠ABD=∠ACD=90°,
∵∠ACB=45°,
∴∠CAM=∠BCD=∠CDN=45°,
∴![]() ,
,![]() ,
,
∵∠ADB=∠ACB=45°,
∴AB=BD,
∵∠ABM+∠DBN=90°=∠BDN+∠DBN,
∴∠ABM=∠BDN,
又∵∠AMB=∠BND=90°,
∴△ABM≌△BDN(AAS),
∴AM=BN,
∴![]() ;
;
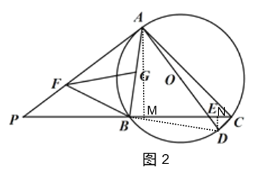
(3)如图3,作AM⊥BC于M,DN⊥BC于N,由(2)可知:![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
设CD=x,则AC=7x,
∵∠AMC=∠DNC=90°,∠ACM=∠DCN=45°,
∴△AMC∽△DNC,
∴![]() ,
,
∵AM⊥BC,DN⊥BC,
∴AM∥DN,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
在Rt△ACD中,AC2+CD2=AD2,
∴![]() ,
,
解得:![]() (负值已舍去),
(负值已舍去),
∴![]() ,
,![]() ,
,![]() ,
,
∵△AMC是等腰直角三角形,
∴![]() ,
,
∴![]() ,
,
∴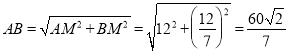 ,
,
∵∠P=∠P,∠PAB=∠PCA=45°,
∴△PAB∽△PCA,
∴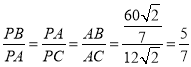 ,
,
设PB=5a,则PA=7a,
由PA2=PB·PC得:![]() ,
,
解得:![]() 或a=0(舍去),
或a=0(舍去),
∴PA=20,
∴![]() ,
,
∴![]() ,
,
过点G作GK⊥FB,过点F作FH⊥BG,
设GK=3b,则BF=FG=5b,
∴FK=4b,
∴BK=b,
∴![]() ,
,
∴BH![]() ,
,
∴ ,
,
∵∠PAB=45°,
∴AH=FH=![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴![]() .
.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列五个结论中:
①2a﹣b<0;②abc<0;③a+b+c<0;④a﹣b+c>0;⑤4a+2b+c>0,
错误的个数有( )
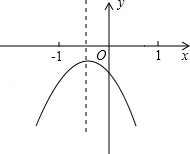
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新型冠状病毒肺炎是一种急性感染性肺炎,其病原体是一种先前未在人体中发现的新型冠状病毒.市民出于防疫的需求,持续抢购防护用品.某药店口罩每袋售价20元,医用酒精每瓶售价15元.
(1)该药店第一周口罩的销售袋数比医用酒精的销售瓶数多100,且第一周这两种防护用品的总销售额为9000元,求该药店第一周销售口罩多少袋?
(2)由于疫情紧张,该药店为了帮助大家共渡难关,第二周口罩售价降低了![]() ,销量比第一周增加了
,销量比第一周增加了![]() ,医用酒精的售价保持不变,销量比第一周增加了
,医用酒精的售价保持不变,销量比第一周增加了![]() ,结果口罩和医用酒精第二周的总销售额比第一周增加了
,结果口罩和医用酒精第二周的总销售额比第一周增加了![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲、乙两个不透明的布袋里,都装有3个大小、材质完全相同的小球,其中甲袋中的小球上分别标有数字0,1,2;乙袋中的小球上分别标有数字﹣1,﹣2,0.现从甲袋中任意摸出一个小球,记其标有的数字为x,再从乙袋中任意摸出一个小球,记其标有的数字为y,以此确定点M的坐标(x,y).
(1)请你用画树状图或列表的方法,写出点M所有可能的坐标;
(2)求点M(x,y)在函数y=﹣![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
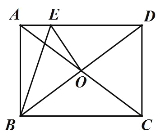
【题目】如图,矩形 ABCD 的对角线 AC 与 BD 交于点 O,点 E 在 AD 上,且 DE=CD,连接 OE,BE, ABE ![]() ACB ,若 AE=2,则 OE 的长为___________.
ACB ,若 AE=2,则 OE 的长为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一次函数y=kx+b与反比例函数y=![]() 的图象交于A(2,4),B(﹣4,n)两点.
的图象交于A(2,4),B(﹣4,n)两点.
(1)分别求出一次函数与反比例函数的表达式;
(2)过点B作BC⊥x轴,垂足为点C,连接AC,求△ACB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把正方形纸片ABCD沿对边上的两点M、N所在的直线对折,使点B落在边CD上的点E处,折痕为MN,其中CE=![]() CD.若AB的长为2,则MN的长为( )
CD.若AB的长为2,则MN的长为( )
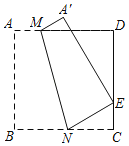
A.3B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线相交于O,E是OD的中点,DF∥AC交CE延长线于点F,连接AF.
(1)求证:四边形AODF是菱形.
(2)若∠AFC=90°,AB=2,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=x2﹣4x+n(x>0)的图象记为G1,将G1绕坐标原点旋转180°得到图象G2,图象G1和G2合起来记为图象G.
(1)若点P(﹣1,2)在图象G上,求n的值.
(2)当n=﹣1时.
①若Q(t,1)在图象G上,求t的值.
②当k≤x≤3(k<3)时,图象G对应函数的最大值为5,最小值为﹣5,直接写出k的取值范围.
(3)当以A(﹣3,3)、B(﹣3,﹣1)、C(2,﹣1)、D(2,3)为顶点的矩形ABCD的边与图象G有且只有三个公共点时,直接写出n的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com