
【题目】如图,已知![]() 是△
是△![]() 的外角
的外角![]() 的平分线,交
的平分线,交![]() 的延长线于点
的延长线于点![]() ,延长
,延长![]() 交△
交△![]() 的外接圆于点
的外接圆于点![]() ,连接
,连接![]() ,
, ![]() .
.
(![]() )求证:
)求证: ![]() .
.
(![]() )已知
)已知![]() ,若
,若![]() 是△
是△![]() 外接圆的直径,
外接圆的直径, ![]() ,求
,求![]() 的长.
的长.

【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:
(1)由四边形AFBC内接于圆可证得∠DAC=∠FBC;由AD平分∠EAC可得∠EAD=∠DAC,结合∠EAD=∠FAB,∠FAB=∠FCB,可得∠FCB=∠DAC,从而可得结论:∠FBC=∠FCB;
(2)由已知条件易证△ABF∽△BDF,由此可得: ![]() 即
即![]() ,从而可解得
,从而可解得![]() ;
; ![]() ,
, ![]() 可解得:FD=6,AD=4;由AB是△ABC外接圆的直径可得∠DFB=∠ACB=∠ACD=90°,由此可解得BD=
可解得:FD=6,AD=4;由AB是△ABC外接圆的直径可得∠DFB=∠ACB=∠ACD=90°,由此可解得BD=![]() ,结合∠D=∠D,可证得△DBF∽△DAC,由此可得CD:DF=AD:BD即可解得CD的值.
,结合∠D=∠D,可证得△DBF∽△DAC,由此可得CD:DF=AD:BD即可解得CD的值.
试题解析:
(![]() )∵四边形
)∵四边形![]() 内接于圆,
内接于圆,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() 是△
是△![]() 的外角
的外角![]() 平分线,
平分线,
∴![]() ,
, ![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() .
.
(![]() )由(
)由(![]() )得
)得![]() ,
,
又∵![]() ,
,
∴△![]() ∽△
∽△![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
, ![]() ,
,
∵![]() 是直径,
是直径,
∴![]() ,
,
∴BD=![]() ,
,
又∵∠D=∠D,
∴△DBF∽△DAC,
∴![]() ,
,
∴![]() CD=24,解得:CD=
CD=24,解得:CD=![]() .
.


科目:初中数学 来源: 题型:
【题目】某城市体育中考项目分为必测项目和选测项目,必测项目为:跳绳、立定跳远;选测项目为50米、实心球、踢毽子三项中任选一项.
(1)每位考生将有 种选择方案;
(2)用画树状图或列表的方法求小颖和小华将选择同种方案的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:

①抛物线与x轴的一个交点为(3,0);②函数y=ax2+bx+c的最大值为6;③抛物线的对称轴是直线![]() ;④在对称轴左侧,y随x增大而增大.从上表可知,以上说法中正确的是____________.(填写序号)
;④在对称轴左侧,y随x增大而增大.从上表可知,以上说法中正确的是____________.(填写序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)画出△A1B1C1沿x轴向右平移4个单位长度后得到的△A2B2C2;
(3)如果AC上有一点M(a,b)经过上述两次变换,那么对应A2C2上的点M2的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数![]() ,
,![]() 定义两种新运算“※”和“
定义两种新运算“※”和“![]() ”:
”: ![]() ※
※![]() ,
,![]() (其中
(其中![]() 为常数,且
为常数,且![]() ,若对于平面直角坐标系
,若对于平面直角坐标系![]() 中的点
中的点![]() ,有点
,有点![]() 的坐标
的坐标![]() ※
※![]() ,
,![]() 与之对应,则称点
与之对应,则称点![]() 的“
的“![]() 衍生点”为点
衍生点”为点![]() .例如:
.例如:![]() 的“2衍生点”为
的“2衍生点”为![]() ,即
,即![]() .
.
(1)点![]() 的“3衍生点”的坐标为 ;
的“3衍生点”的坐标为 ;
(2)若点![]() 的“5衍生点”
的“5衍生点” ![]() 的坐标为
的坐标为![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)若点![]() 的“
的“![]() 衍生点”为点
衍生点”为点![]() ,且直线
,且直线![]() 平行于
平行于![]() 轴,线段
轴,线段![]() 的长度为线段
的长度为线段![]() 长度的3倍,求
长度的3倍,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,已知A(2,2)、B(4,0),若在x轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是( )
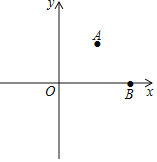
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
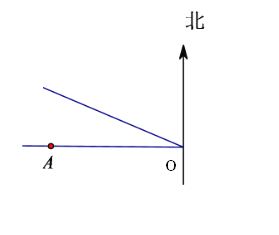
【题目】某台风中心位于O点,台风中心以![]()
![]() 的速度向北偏西
的速度向北偏西![]() 方向移动,在半径
方向移动,在半径![]() 的范围内将受影响,城市A在O点正西方向与O点相距
的范围内将受影响,城市A在O点正西方向与O点相距![]() 处,试问:
处,试问:
(1)![]() 市是否会受此台风影响,并说明理由;
市是否会受此台风影响,并说明理由;
(2)如受影响,则受影响的时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售有甲、乙两种商品,甲商品每件进价10元,售价15元;乙商品每件进价30元,售价40元.
(1)若该超市一次性购进两种商品共60件,且恰好用去1600元,问购进甲、乙两种商品各多少件?
(2)若该超市要使两种商品共60件的购进费用不超过1240元,且总利润(利润=售价-进价)不少于450元,请你帮助该超市设计相应的进货方案,并指出使该超市利润最大的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
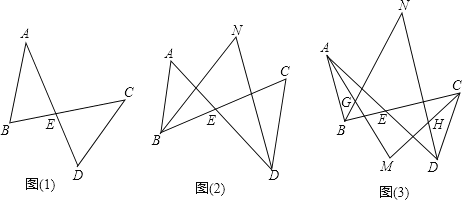
【题目】图![]() 是我们常见的基本图形,我们可以称之为“8”字形
是我们常见的基本图形,我们可以称之为“8”字形![]() “8”字形有一个重要的性质如下:
“8”字形有一个重要的性质如下:
![]() 利用这个性质并结合你所学的知识解决以下问题:
利用这个性质并结合你所学的知识解决以下问题:
![]() 如图
如图![]() ,
,![]() ,
,![]() ,直接写出
,直接写出![]() 的度数为______;
的度数为______;
![]() 如图
如图![]() ,若BN、DN分别是
,若BN、DN分别是![]() 、
、![]() 的角平分线,BN与DN交于点N、且
的角平分线,BN与DN交于点N、且![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
![]() 如图
如图![]() ,若AM、BN、CM、DN分别是
,若AM、BN、CM、DN分别是![]() 、
、![]() 、
、![]() 和
和![]() 的角平分线,AM与CM、BN交于点M、G,DN与BN、CM交于点N、H,且
的角平分线,AM与CM、BN交于点M、G,DN与BN、CM交于点N、H,且![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com