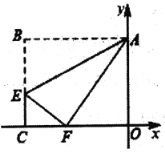
【题目】如图，在平面直角坐标系中，长方形
的边
，
分别在
轴，
轴上，点
在边
上，将该长方形沿
折叠，点
恰好落在边
上的点
处，若
，
，则所在直线的表达式为__________．
【答案】
【解析】
设CE=a，根据勾股定理可以得到CE、OF的长度，再根据点E在第二象限，从而可以得到点E的坐标．然后利用待定系数法求出AE所在直线的解析式．
解：设CE=a，则BE=8-a，
由折叠的性质可得：EF=BE=8-a，AB=AF
∵∠ECF=90°，CF=4，
∴a2+42=（8-a）2，
解得，a=3，
∴OE=3
设OF=b，则OC=AB=AF=4+b
∵∠ACF=90°，OA=8，
∴b2+82=（b+4）2，
∴b=6，∴OF=6
∴OC=CF+OF=10，
∴点E的坐标为（-10，3），
设AE所在直线的解析式为y=kx+b（k≠0）．
将E（-10，3），A（0，8）代入y=kx+b
得
，解得
∴AE所在直线的解析式为：
故答案为：
科目：初中数学 来源： 题型：
【题目】列方程组解应用题：用3辆
型车和2辆
型车载满货物一次可运货17吨；用2辆型车和3辆型车载满货物一次可运货18吨,某物流公司现有35吨货物,计划同时租用型车
辆,型车
辆,一次运完,且恰好每辆车都载满货物.
（1）1辆型车和1辆型车都载满货物一次可分别运货多少吨？
（2）若型车每辆需租金200元/次,型车每辆需租金240元/次,请你帮该物流设计最省钱的租车方案,并求出最少租车费.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠B=90°，BC=8 AB=6cm，动点P从点A开始沿边AB向点B以1cm/s的速度移动，动点Q从点B开始沿边BC向点C以2cm/s的速度移动．若P，Q两点分别从A，B两点同时出发，在运动过程中，△PBQ的最大面积是（ ）
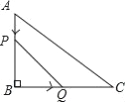
A. 18cm2 B. 12cm2 C. 9cm2 D. 3cm2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，长方体的长为15，宽为10，高为20，点B离点C的距离为5，一只蚂蚁如果要沿着长方体的表面从点A爬到点B，需要爬行的最短距离是__________
查看答案和解析>>
科目：初中数学 来源： 题型：
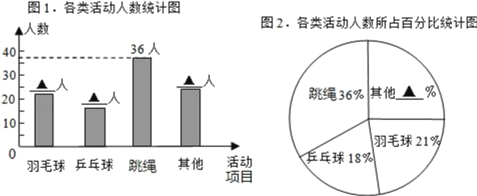
【题目】学校统筹安排大课间体育活动，在各班随机选取了一部分学生，分成四类活动：“跳绳”、“羽毛球”、“乒乓球”、“其他”进行调查，整理收集到的数据，绘制成如图的两幅统计图．
（1）学校采用的调查方式是 ；学校在各班随机选取了 名学生；
（2）补全统计图中的数据：羽毛球 人、乒乓球 人、其他 %；
（3）该校共有900名学生，请估计喜欢“跳绳”的学生人数．
查看答案和解析>>
科目：初中数学 来源： 题型：
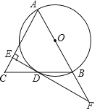
【题目】如图，
是
的直径，
是的弦，延长到点
，使
，连结
，过点
作
，垂足为
，交的延长线于点
．
求证：
为的切线；
猜想线段
、
、之间的数量关系，并证明你的猜想；
若
，
，求线段的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】计算下列各题．
①（x2+3）（3x2﹣1）
②（4x2y﹣8x3y3）÷（﹣2x2y）
③[（m+3）（m﹣3）]2
④10﹣2×100+105÷103
⑤
⑥
，其中x满足x2﹣x﹣1＝0．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AC平分钝角∠BAE交过B点的直线于点C，BD平分∠ABC交AC于点D，且∠BAD+∠ABD＝90°．
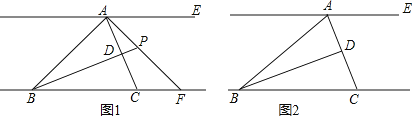
（1）求证：AE∥BC；
（2）点F是射线BC上一动点（点F不与点B，C重合），连接AF，与射线BD相交于点P．
（ⅰ）如图1，若∠ABC＝45°，AF⊥AB，试探究线段BF与CF之间满足的数量关系；
（ⅱ）如图2，若AB＝10，S△ABC＝30，∠CAF＝∠ABD，求线段BP的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
