
| 5 |
| 2 |
| a+0 |
| 2 |
| 5 |
| 2 |
| a+c |
| 2 |
| 3 |
| 2 |
| 7 |
| 3 |


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
| 4 |
| 3 |
| 2x+m |
| x-2 |
| A、②③ | B、①② | C、①③ | D、①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:
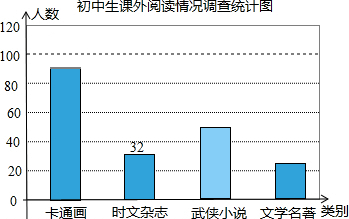 4月23日是“世界读书日”,今年世界读书日的主题是“阅读,让我们的世界更丰富”.某校随机调查了部分学生,就“你最喜欢的图书类别”(只选一项)对学生课外阅读的情况作了调查统计,将调查结果统计后绘制成如下统计表和条形统计图.请根据统计图表提供的信息解答下列问题:
4月23日是“世界读书日”,今年世界读书日的主题是“阅读,让我们的世界更丰富”.某校随机调查了部分学生,就“你最喜欢的图书类别”(只选一项)对学生课外阅读的情况作了调查统计,将调查结果统计后绘制成如下统计表和条形统计图.请根据统计图表提供的信息解答下列问题:| 种类 | 频数 | 频率 |
| 卡通画 | a | 0.45 |
| 时文杂志 | b | 0.16 |
| 武侠小说 | 50 | c |
| 文学名著 | d | e |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 3 |
| a-3 |
| 3a2-6a |
| 5 |
| a-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地,乙骑摩托车从B地到A地,到达A地后立即按原路返回,是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地,乙骑摩托车从B地到A地,到达A地后立即按原路返回,是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com