【题目】如图，在平面直角坐标系中，
的顶点均在正方形的格点上，点D的坐标是
，点A的坐标是
（1）将平移后使点C与点D重合，点A、B分别与点E、F重合，画出
，并直接写出E、F的坐标．
（2）若AB上的点M坐标为
，则平移后的对应点
的坐标为_______（用含x、y的代数式表示）
（3）求的面积.
快捷英语周周练系列答案科目：初中数学 来源： 题型：
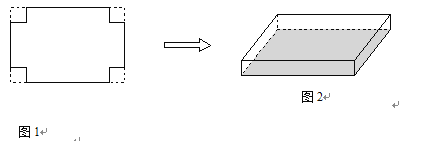
【题目】（本题满分8分）一张长为30cm，宽20cm的矩形纸片，如图1所示，将这张纸片的四个角各剪去一个边长相同的正方形后，把剩余部分折成一个无盖的长方体纸盒，如图1所示，如果折成的长方体纸盒的底面积为264cm2，求剪掉的正方形纸片的边长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】解决下列两个问题：
（1）如图1，在△ABC中，AB＝3，AC＝4，BC＝5．EF垂直且平分BC．点P在直线EF上，直接写出PA+PB的最小值，并在图中标出当PA+PB取最小值时点P的位置；
解：PA+PB的最小值为 ．
（2）如图2．点M、N在∠BAC的内部，请在∠BAC的内部求作一点P，使得点P到∠BAC两边的距离相等，且使PM＝PN．（尺规作图，保留作图痕迹，无需证明）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下列材料并解决有关问题：
我们知道，|m|=
．现在我们可以用这一结论来化简含有绝对值的代
数式，如化简代数式|m+1|+|m﹣2|时，可令 m+1=0 和 m﹣2=0，分别求得 m=﹣1，m=2（称﹣1，2 分别为|m+1|与|m﹣2|的零点值）．在实数范围内， 零点值 m=﹣1 和 m=2 可将全体实数分成不重复且不遗漏的如下 3 种情况：
（1）m＜﹣1；（2）﹣1≤m＜2；（3）m≥2．从而化简代数式|m+1|+|m﹣2| 可分以下 3 种情况：
（1）当 m＜﹣1 时，原式=﹣（m+1）﹣（m﹣2）=﹣2m+1；
（2）当﹣1≤m＜2 时，原式=m+1﹣（m﹣2）=3；
（3）当 m≥2 时，原式=m+1+m﹣2=2m﹣1．
综上讨论，原式=
通过以上阅读，请你解决以下问题：
（1）分别求出|x﹣5|和|x﹣4|的零点值；
（2）化简代数式|x﹣5|+|x﹣4|；
（3）求代数式|x﹣5|+|x﹣4|的最小值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】学校准备添置一批计算机．
方案1：到商家直接购买，每台需要7000元；
方案2：学校买零部件组装，每台需要6000元，另外需要支付安装工工资等其它费用合计3000元．设学校需要计算机x台，方案1与方案2的费用分别为
、
元．
分别写出、的函数关系式；
当学校添置多少台计算机时，两种方案的费用相同？
采用哪一种方案较省钱？说说你的理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，∠A=∠B，AE=BE，点D在AC边上，∠1=∠2，AE和BD相交于点O．
（1）求证：△AEC≌△BED；
（2）若∠1=42°，求∠BDE的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列命题：①若
，则
；②直角三角形的两个锐角互余：③如果
，那么
④
个角都是直角的四边形是正方形.其中，原命题和逆命题均为真命题的有（ ）
A.
个B.
个C.
个D.
个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.
(1)如果AC=6cm,BC=8cm,试求△ACD的周长；
(2)如果∠CAD:∠BAD=1:2,求∠B的度数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙两名采购员同去一家饲料公司购买两次饲料．两次饲料的价格分别为
元/千克和
元/千克（、都为正数，且
），两名采购员的购货方式不同，其中甲每次购买800千克；乙每次用去800元，而不管购买多少饲料．
（1）用含、的代数式表示甲、乙两名采购员两次购买饲料的平均单价各是多少？
（2）若规定：谁两次购买饲料的平均单价低，谁的购货方式合算，请你判断甲、乙两名采购员购货方式哪个更合算？说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
