
【题目】在平面直角坐标系xOy中,抛物线y=﹣x2+2mx﹣m2+1的对称轴是直线x=1.
(1)求抛物线的表达式;
(2)点D(n,y1),E(3,y2)在抛物线上,若y1<y2,请直接写出n的取值范围;
(3)设点M(p,q)为抛物线上的一个动点,当﹣1<p<2时,点M关于y轴的对称点都在直线y=kx﹣4的上方,求k的取值范围.
【答案】(1)抛物线的解析式为y=﹣x2+2x.(2)当n<﹣1或n>3时,y1<y2.
(3)∴k的取值范围是﹣2≤k≤1.
【解析】
试题分析:(1)由抛物线的对称轴方程可求得m=1,从而可求得抛物线的表达式;
(2)将x=3代入抛物线的解析式,可求得y2=3,将y=3代入抛物线的解析式可求得x1=﹣1,x2=3,由抛物线的开口向下,可知当当n<﹣1或n>3时,y1<y2;
(3)先根据题意画出点M关于y轴对称点M′的轨迹,然后根据点M关于y轴的对称点都在直线y=kx﹣4的上方,列出关于k的不等式组即可求得k的取值范围.
试题解析:(1)∵抛物线的对称轴为x=1,∴x=﹣![]() =1.
=1.
解得:m=1.∴抛物线的解析式为y=﹣x2+2x.
(2)将x=3代入抛物线的解析式得y=﹣32+2×3=﹣3.
将y=﹣3代入得:﹣x2+2x=﹣3.解得:x1=﹣1,x2=3.
∵a=﹣1<0,∴当n<﹣1或n>3时,y1<y2.
(3)设点M关于y轴对称点为M′,则点M′运动的轨迹如图所示:
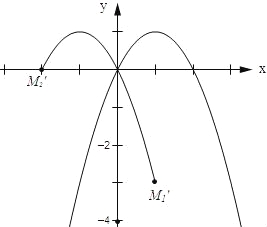
∵当P=﹣1时,q=﹣(﹣1)2+2×(﹣1)=﹣3.∴点M关于y轴的对称点M1′的坐标为(1,﹣3).
∵当P=2时,q=﹣22+2×2=0,∴点M关于y轴的对称点M2′的坐标为(﹣2,0).
①当k<0时,∵点M关于y轴的对称点都在直线y=kx﹣4的上方,∴﹣2k﹣4≤0.
解得:k≥﹣2.
②当k>0时,∵点M关于y轴的对称点都在直线y=kx﹣4的上方,
∴k﹣4≤﹣3.解得;k≤1.
∴k的取值范围是﹣2≤k≤1.


科目:初中数学 来源: 题型:
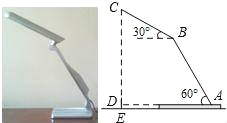
【题目】如图,放置在水平桌面上的台灯的灯臂AB长为40cm,灯罩BC长为30cm,底座厚度为2cm,灯臂与底座构成的∠BAD=60°.使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm?
(结果精确到0.1cm,参考数据:![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】上星期我市某水果价格呈上升趋势,某超市第一次用1000元购进的这种水果很快卖完,第二次又用960元购进该水果,但第二次每千克的进价是第一次进价的1.2倍,购进数量比第一次少了20千克.
(1)求第一次购进这种水果每千克的进价是多少元?
(2)本星期受天气影响,批发市场这种水果的数量有所减少.该超市所购进的数量比上星期所进购的总量减少了4a%,每千克的进价在上星期第二次进价的基础上上涨5a%,结果本星期进货总额比上星期进货总额少16元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P(x,y)在第二象限,且点P到x轴、y轴的距离分别为3,5,则点P的坐标( )
A. (﹣5,3) B. (5,﹣3) C. (﹣3,5) D. (3,﹣5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践与探索
(1)填空: ![]() =______;
=______; ![]() =______;
=______; ![]() =______;
=______; ![]() ______;
______;
(2)观察第(1)题的计算结果回答: ![]() 一定等于
一定等于![]() 吗?你发现其中的规律了吗?请把你观察到的规律归纳出来 。
吗?你发现其中的规律了吗?请把你观察到的规律归纳出来 。
(3)利用你总结的规律计算: ![]() .(2<x<3)
.(2<x<3)
查看答案和解析>>
科目:初中数学 来源: 题型:
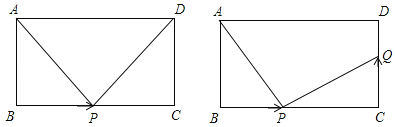
【题目】如图,在长方形ABCD中,AB=CD=6cm,BC=10cm,点P从点B出发,以2cm/秒的速度沿BC向点C运动,设点P的运动时间为t秒:
(1)PC=______cm.(用t的代数式表示)
(2)当t为何值时,△ABP≌△DCP?
(3)当点P从点B开始运动,同时,点Q从点C出发,以v cm/秒的速度沿CD向点D运动,是否存在这样v的值,使得△ABP与△PQC全等?若存在,请求出v的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列方程变形中,正确的是( )
A.方程3x﹣2=2x+1,移项,得3x﹣2x=﹣1+2
B.方程3﹣x=2﹣5(x﹣1),去括号,得3﹣x=2﹣5x﹣1
C.方程 ![]() t=
t= ![]() ,系数化为1,得t=1
,系数化为1,得t=1
D.方程 ![]() =
= ![]() ,去分母,得5(x﹣1)=2x
,去分母,得5(x﹣1)=2x
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(+26)﹣(﹣26)﹣6
(2)(﹣4)× ![]() ÷8
÷8
(3)( ![]() ﹣
﹣ ![]() +
+ ![]() )×(﹣36)
)×(﹣36)
(4)(﹣2)2﹣[﹣32+(﹣11)]×(﹣2)÷(﹣1)2016 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com