
【题目】小李在学习了定理“直角三角形斜边上的中线等于斜边的一半”之后做了如下思考,请你帮他完成如下问题:
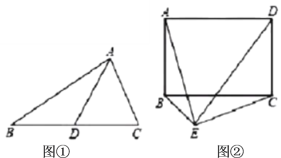
(1)他认为该定理有逆定理:“如果一个三角形某条边上的中线等于该边长的一半,那么这个三角形是直角三角形”应该成立.即如图①,在![]() 中,
中,![]() 是
是![]() 边上的中线,若
边上的中线,若![]() ,求证:
,求证:![]() .
.
(2)如图②,已知矩形![]() ,如果在矩形外存在一点
,如果在矩形外存在一点![]() ,使得
,使得![]() ,求证:
,求证:![]() .(可以直接用第(1)问的结论)
.(可以直接用第(1)问的结论)
(3)在第(2)问的条件下,如果![]() 恰好是等边三角形,请求出此时矩形的两条邻边
恰好是等边三角形,请求出此时矩形的两条邻边![]() 与
与![]() 的数量关系.
的数量关系.
【答案】(1)详见解析;(2)详见解析;(3)![]()
【解析】
(1)利用等腰三角形的性质和三角形内角和即可得出结论;
(2)先判断出OE=![]() AC,即可得出OE=
AC,即可得出OE=![]() BD,即可得出结论;
BD,即可得出结论;
(3)先判断出△ABE是底角是30°的等腰三角形,即可构造直角三角形即可得出结论.
(1)∵AD=BD,
∴∠B=∠BAD,
∵AD=CD,
∴∠C=∠CAD,
在△ABC中,∠B+∠C+∠BAC=180°,
∴∠B+∠C+∠BAD+∠CAD=∠B+∠C+∠B+∠C=180°
∴∠B+∠C=90°,
∴∠BAC=90°,
(2)如图②,连接![]() 与
与![]() ,交点为
,交点为![]() ,连接
,连接![]()
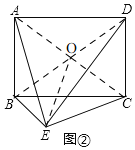
![]() 四边形
四边形![]() 是矩形
是矩形
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(3)如图3,过点![]() 做
做![]() 于点
于点![]()

![]() 四边形
四边形![]() 是矩形
是矩形
![]() ,
,![]()
![]() 是等边三角形
是等边三角形
![]() ,
,![]()
由(2)知,![]()
![]()
![]()
![]() 在
在![]() 中,
中,![]()
![]() ,
,![]()
![]()
![]()
![]()


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
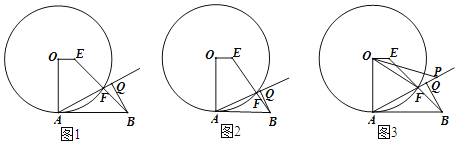
【题目】如图,OA是⊙O的半径,点E为圆内一点,且OA⊥OE,AB是⊙O的切线,EB交⊙O于点F,BQ⊥AF于点Q.
(1)如图1,求证:OE∥AB;
(2)如图2,若AB=AO,求![]() 的值;
的值;
(3)如图3,连接OF,∠EOF的平分线交射线AF于点P,若OA=2,cos∠PAB=![]() ,求OP的长.
,求OP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对某一个函数给出如下定义:若存在实数![]() ,对于函数图象上横坐标之差为1的任意两点
,对于函数图象上横坐标之差为1的任意两点![]() ,
,![]() ,
,![]() 都成立,则称这个函数是限减函数,在所有满足条件的
都成立,则称这个函数是限减函数,在所有满足条件的![]() 中,其最大值称为这个函数的限减系数.例如,函数
中,其最大值称为这个函数的限减系数.例如,函数![]() ,当
,当![]() 取值
取值![]() 和
和![]() 时,函数值分别为
时,函数值分别为![]() ,
,![]() ,故
,故![]() ,因此函数
,因此函数![]() 是限减函数,它的限减系数为
是限减函数,它的限减系数为![]() .
.
(1)写出函数![]() 的限减系数;
的限减系数;
(2)![]() ,已知
,已知![]() (
(![]() )是限减函数,且限减系数
)是限减函数,且限减系数![]() ,求
,求![]() 的取值范围.
的取值范围.
(3)已知函数![]() 的图象上一点
的图象上一点![]() ,过点
,过点![]() 作直线
作直线![]() 垂直于
垂直于![]() 轴,将函数
轴,将函数![]() 的图象在点
的图象在点![]() 右侧的部分关于直线
右侧的部分关于直线![]() 翻折,其余部分保持不变,得到一个新函数的图象,如果这个新函数是限减函数,且限减系数
翻折,其余部分保持不变,得到一个新函数的图象,如果这个新函数是限减函数,且限减系数![]() ,直接写出
,直接写出![]() 点横坐标
点横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(Ⅰ)如图1,在菱形![]() 中,已知
中,已知![]() ,
,![]() ,抛物线
,抛物线![]() (
(![]() )经过
)经过![]() ,
,![]() ,
,![]() 三点.
三点.
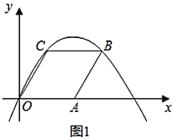
(1)点![]() 的坐标为__________,点
的坐标为__________,点![]() 的坐标为__________;
的坐标为__________;
(2)求抛物线的解析式.
(Ⅱ)如图2,点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 的中点,直线
的中点,直线![]() 垂直
垂直![]() 于点
于点![]() ,点
,点![]() 在直线
在直线![]() 上.
上.
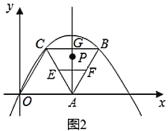
(3)当![]() 的值最小时,则点
的值最小时,则点![]() 的坐标为____________;
的坐标为____________;
(4)在(3)的条件下,连接![]() 、
、![]() 、
、![]() 得
得![]() ,问在抛物线上是否存在点
,问在抛物线上是否存在点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,请求出点
相似?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象相交于点A(1,4)和点B(n,
的图象相交于点A(1,4)和点B(n,![]() ).
).
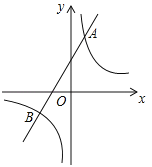
(1)求反比例函数和一次函数的解析式;
(2)当一次函数的值小于反比例函数的值时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
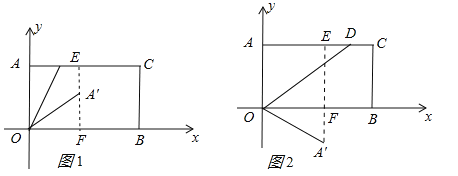
【题目】(2017江西省,第12题,3分)已知点A(0,4),B(7,0),C(7,4),连接AC,BC得到矩形AOBC,点D的边AC上,将边OA沿OD折叠,点A的对应边为A'.若点A'到矩形较长两对边的距离之比为1:3,则点A'的坐标为______________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
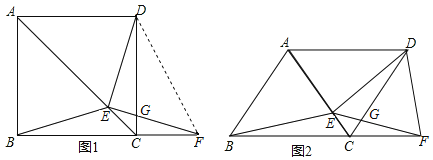
【题目】如图1,在正方形![]() 中,
中,![]() 是对角线
是对角线![]() 上的一点,点
上的一点,点![]() 在
在![]() 的延长线上,
的延长线上,![]() 交
交![]() 于
于![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)连接![]() ,若
,若![]() ,求
,求![]() ;
;
(3)如图2,若把正方形![]() 改为菱形
改为菱形![]() ,其他条件不变,当
,其他条件不变,当![]() 时,猜想
时,猜想![]() 与
与![]() 的数量关系,并证明你的猜想.
的数量关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.
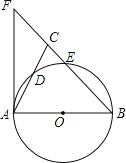
(1)求证:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE的长.
,CE:EB=1:4,求CE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com