【题目】（2017江西省，第12题，3分）已知点A（0，4），B（7，0），C（7，4），连接AC，BC得到矩形AOBC，点D的边AC上，将边OA沿OD折叠，点A的对应边为A'．若点A'到矩形较长两对边的距离之比为1：3，则点A'的坐标为______________________________________．
【答案】（
，3）或（
，1）或（
，﹣2）．
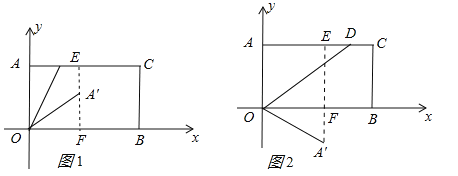
【解析】∵点A（0，4），B（7，0），C（7，4），∴BC=OA=4，OB=AC=7，分两种情况：
（1）当点A'在矩形AOBC的内部时，过A'作OB的垂线交OB于F，交AC于E，如图1所示：
①当A'E：A'F=1：3时，∵A'E+A'F=BC=4，∴A'E=1，A'F=3，由折叠的性质得：OA'=OA=4，在Rt△OA'F中，由勾股定理得：OF=
=，∴A'（，3）；
②当A'E：A'F=3：1时，同理得：A'（，1）；
（2）当点A'在矩形AOBC的外部时，此时点A'在第四象限，过A'作OB的垂线交OB于F，交AC于E，如图2所示：∵A'F：A'E=1：3，则A'F：EF=1：2，∴A'F=
EF=BC=2，由折叠的性质得：OA'=OA=4，在Rt△OA'F中，由勾股定理得：OF=
=，∴A'（，﹣2），
故答案为：（，3）或（，1）或（，﹣2）．
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，抛物线y=-
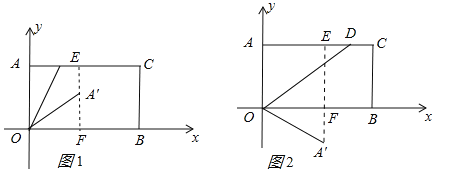
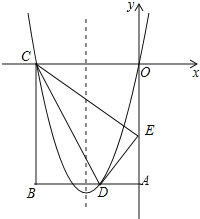
x2+
x+3与x轴交于A，B两点（点A在点B左侧），与y轴交于点C：连接BC，点P为线段BC上方抛物线上的一动点，连接OP交BC于点Q．
（1）如图1，当
值最大时，点E为线段AB上一点，在线段BC上有两动点M，N（M在N上方），且MN=1，求PM+MN+NE-
BE的最小值；
（2）如图2，连接AC，将△AOC沿射线CB方向平移，点A，C，O平移后的对应点分别记作A1，C1，O1，当C1B=O1B时，连接A1B、O1B，将△A1O1B绕点O1沿顺时针方向旋转90°后得△A2O1B1在直线x=
上是否存在点K，使得△A2B1K为等腰三角形？若存在，直接写出点K的坐标；不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某数学活动小组在研究三角形拓展图形的性质时，经历了如下过程：
●操作发现
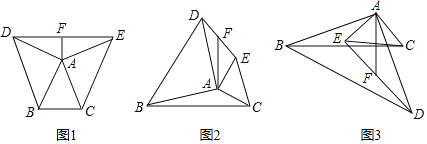
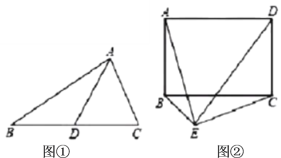
在等腰△ABC中，AB＝AC，分别以AB和AC为腰，向△ABC的外侧作等腰直角三角形，如图①所示，连接DE，其中F是DE的中点，连接AF，则下列结论正确的是 （填序号即可）
①AF＝
BC：②AF⊥BC；③整个图形是轴对称图形；④DE∥BC、
●数学思考
在任意△ABC中，分别以AB和AC为腰，向△ABC的外侧作等腰直角三角形，如图②所示，连接DE，其中F是DE的中点，连接AF，则AF和BC有怎样的数量和位置关系？请给出证明过程
●类比探索
在任意△ABC中，仍分别以AB和AC为腰，向△ABC的内侧作等腰直角三角形，如图③所示，连接DE，其中F是DE的中点，连接AF，试判断AF和BC的数量和位置关系是否发生改变？并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小李在学习了定理“直角三角形斜边上的中线等于斜边的一半”之后做了如下思考，请你帮他完成如下问题：
（1）他认为该定理有逆定理：“如果一个三角形某条边上的中线等于该边长的一半，那么这个三角形是直角三角形”应该成立.即如图①，在
中，
是
边上的中线，若
，求证：
.
（2）如图②，已知矩形
，如果在矩形外存在一点
，使得
，求证：
.（可以直接用第（1）问的结论）
（3）在第（2）问的条件下，如果
恰好是等边三角形，请求出此时矩形的两条邻边
与的数量关系.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为配合全市“禁止焚烧秸秆”工作，某学校举行了“禁止焚烧秸秆，保护环境，从我做起”为主题的演讲比赛． 赛后组委会整理参赛同学的成绩，并制作了如下不完整的频数分布表和频数分布直方图．
分数段（分数为x分） | 频数 | 百分比 |
60≤x＜70 | 8 | 20% |
70≤x＜80 | a | 30% |
80≤x＜90 | 16 | b% |
90≤x＜100 | 4 | 10% |
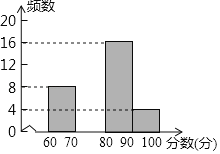
请根据图表提供的信息，解答下列问题：
（1）表中的a＝ ，b＝ ；请补全频数分布直方图；
（2）若用扇形统计图来描述成绩分布情况，则分数段70≤x＜80对应扇形的圆心角的度数是 ；
（3）竞赛成绩不低于90分的4名同学中正好有2名男同学，2名女同学． 学校从这4名同学中随机抽2名同学接受电视台记者采访，则正好抽到一名男同学和一名女同学的概率为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
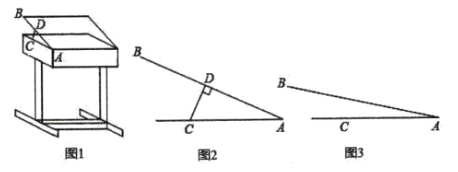
【题目】某课桌生产厂家研究发现，倾斜12°至24°的桌面有利于学生保持躯体自然姿势．根据这一研究，厂家决定将水平桌面做成可调节角度得桌面．新桌面的设计图如图1，
可绕点
旋转，在点
处安装一根长度一定且处固定，可旋转的支撑臂
，
．
（1）如图2，当
时，
，求支撑臂的长；
（2）如图3，当
时，求
的长．（结果保留根号）
（参考数据：
，
，
，
）
查看答案和解析>>
科目：初中数学 来源： 题型：
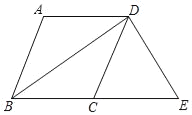
【题目】如图，在四边形ABCD中，AD∥BC，BA＝BC，BD平分∠ABC．
（1）求证：四边形ABCD是菱形；
（2）过点D作DE⊥BD，交BC的延长线于点E，若BC＝5，BD＝8，求四边形ABED的周长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】由甲、乙两个工程队承包某校校园绿化工程，甲、乙两队单独完成这项工程所需时间比是3︰2，两队合做6天可以完成．
（1）求两队单独完成此项工程各需多少天?
（2）此项工程由甲、乙两队合做6天完成任务后，学校付给他们20000元报酬，若
按各自完成的工程量分配这笔钱，问甲、乙两队各得到多少元?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形OABC中，OA＝5，AB＝4，点D为边AB上一点，将△BCD沿直线CD折叠，使点B恰好落在边OA上的点E处，分别以OC，OA所在的直线为x轴，y轴建立平面直角坐标系．
（1）求OE的长及经过O，D，C三点抛物线的解析式；
（2）一动点P从点C出发，沿CB以每秒2个单位长度的速度向点B运动，同时动点Q从E点出发，沿EC以每秒1个单位长度的速度向点C运动，当点P到达点B时，两点同时停止运动，设运动时间为t秒，当t为何值时，DP＝DQ；
（3）若点N在（1）中抛物线的对称轴上，点M在抛物线上，是否存在这样的点M与点N，使M，N，C，E为顶点的四边形是平行四边形？若存在，请求出M点坐标；若不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com