
����Ŀ��Ϊ���ȫ�С���ֹ���սոѡ�������ijѧУ�����ˡ���ֹ���սոѣ�������������������Ϊ������ݽ������� ������ί����������ͬѧ�ijɼ��������������²�������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ��
�����Σ�����Ϊx���� | Ƶ�� | �ٷֱ� |
60��x��70 | 8 | 20% |
70��x��80 | a | 30% |
80��x��90 | 16 | b% |
90��x��100 | 4 | 10% |
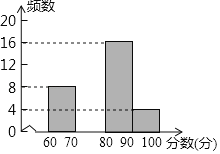
�����ͼ���ṩ����Ϣ������������⣺
��1�����е�a�� ��b�� ���벹ȫƵ���ֲ�ֱ��ͼ��
��2����������ͳ��ͼ�������ɼ��ֲ�������������70��x��80��Ӧ���ε�Բ�ĽǵĶ����� ��
��3�������ɼ�������90�ֵ�4��ͬѧ��������2����ͬѧ��2��Ůͬѧ�� ѧУ����4��ͬѧ�������2��ͬѧ���ܵ���̨���߲ɷã������ó鵽һ����ͬѧ��һ��Ůͬѧ�ĸ���Ϊ ��
���𰸡���1��12��40������ȫֱ��ͼ����������2��108������3��![]() ��
��
��������
��1�����ȸ��ݷ�����Ϊ60��x��70��Ƶ������Ƶ�������������Ȼ���ȥ����С���Ƶ���������a��ֵ�������������ͷ�����Ϊ80��x��90��Ƶ���������b��ֵ�����������a��ֵ�����ɲ�ȫƵ���ֲ�ֱ��ͼ��
��2����360�������Ӧ��������ռ�İٷֱȼ������Բ�ĽǵĶ�����
��3���б������еȿ��ܵĽ���оٳ����������ø��ʹ�ʽ��⼴�ɣ�
�⣺��1���߷�����Ϊ60��x��70��Ƶ��Ϊ8��ռ20%����������Ϊ8��20%��40�ˣ�
��a��40��8��16��4��12��b%��![]() ��100%��40%����b��40��
��100%��40%����b��40��
�ʴ�Ϊ��12��40��
��ȫƵ���ֲ�ֱ��ͼ���£�
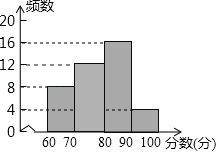
��2���߷�����Ϊ70��x��80��ռ�İٷֱ�Ϊ30%��
�������70��x��80��Ӧ���ε�Բ�ĽǵĶ���Ϊ��360����30%��108����
�ʴ�Ϊ��108����
��3����A��B��ʾ2����������a��b��ʾ2��Ů�����б��ã�
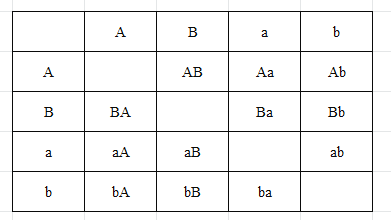
�߹���12�ֵȿ��ܵĽ��������һ��һŮ����8�������
��P�����ó鵽һ��һŮ����![]() ��
��
�ʴ�Ϊ��![]() ��
��


 ͬ����ϰ���ϴ�ѧ������ϵ�д�
ͬ����ϰ���ϴ�ѧ������ϵ�д� ͬ����ϰ���ϴ�ѧ������ϵ�д�
ͬ����ϰ���ϴ�ѧ������ϵ�д� ����ϰ�⽭��ϵ�д�
����ϰ�⽭��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�ܣ�����ѧУ���ڽ�������ؽ����п�ģ�⿼�ԣ�ѧ����ͨ��ģ�⿼���������Լ���״̬���˽��Լ���ѧҵˮƽ��ij��ѧ������������ͨ���˴��п�ģ��ijɼ���Ԥ���п��ĸ�����������������ȫ�꼶�����ȡ���У�Ů��40��ѧ���ijɼ�������Ϊ80�֣�Ů���ɼ�����ͷ�Ϊ45�֣����������ݽ����������������������沿����Ϣ��
�������ɼ�����ͳ��ͼ��Ů���ɼ�Ƶ���ֲ�ֱ��ͼ���£������ݷ���ΪA�飺x<50��B�飺50��x<60��C�飺60��x<70��D�飺70��x��80��

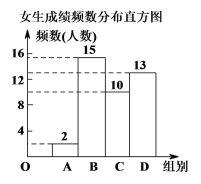
������C����ȫ��15��ѧ���ijɼ�Ϊ��
63��69��64��62��68��69��65��69��65��66��67��61��67��66��69��
���������ݵ�ƽ��������λ���������������ʣ������λ���֣����±���ʾ��
ƽ���� | ��λ�� | ���� | ������ | ���� | |
���� | 70 | b | c | 25% | 32 |
�� | 70 | 68 | 78 | 15% | d |
��1������ͳ��ͼA��ѧ��������Ӧ��Բ�Ľ����Ķ���Ϊ ����λ��b= ������c= ������d= ��
��2��ͨ�����ϵ����ݷ���������Ϊ ����������������Ů�������������ɼ����ã���˵�����ɣ�
�� ���� ��
��3�����ɼ���70�֣�����70�֣�����Ϊ���㣬������Ƹ�У1200��ѧ���д˴ο����������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ˮ������Ϊ��ѡ����Ӧ�г������С���������磬������������ͬ������£�������Ʒ�ֵ�С�����������300��ֱ���ֲ�ڼס�������������г���Ϊ��ע�IJ����Ͳ������ȶ��Խ����˳������飬��������:
�ռ����ݴӼס������������зֱ�����ռ�����ͬ����������25��������������С�������ĸ�����
�ף�26��32��40��51��44��74��44��63��73��74��81��54��62��41��33��54��43��34��51��63��64��73��64��54��33
�ң�27��35��46��55��48��36��47��68��82��48��57��66��75��27��36��57��57��66��58��61��71��38��47��46��71
�������ݰ����·��������������ݣ�
������x�� �������꣩ ���� | 25��x��35 | 35��x��45 | 45��x��55 | 55��x��65 | 65��x��75 | 75��x��85 |
�� | 5 | �� �� | 5 | �� �� | 4 | 1 |
�� | 2 | 4 | �� �� | 6 | 5 | 2 |
��˵����45������Ϊ�������ϸ�45��������Ϊ�����ϸ�����45��x��65��Ϊ�������ã�65��x��85��Ϊ�������㣩
�������������������ݵ�ƽ�����������ͷ������±���ʾ��
���� | ƽ���� | ���� | ���� |
�� | 53 | �� �� | 236.24 |
�� | 53 | 57 | 215.04 |
����
��1����ȫ��������
��2�������ƶϳ��� �������С����������Ʒ�ָ���Ӧ�г���������Ϊ�� �������ٴ�������ͬ�ĽǶ�˵���ƶϵĺ����ԣ���
��3�������Ҵ����300��С�����������в���������ж����ꣿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ͼ1��������![]() �У���֪
�У���֪![]() ��
��![]() ��������
��������![]() ��
��![]() ������
������![]() ��
��![]() ��
��![]() ���㣮
���㣮
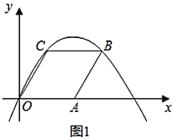
��1����![]() ������Ϊ__________����
������Ϊ__________����![]() ������Ϊ__________��
������Ϊ__________��
��2���������ߵĽ���ʽ��
������ͼ2����![]() ��
��![]() ���е㣬��
���е㣬��![]() ��
��![]() ���е㣬ֱ��
���е㣬ֱ��![]() ��ֱ
��ֱ![]() �ڵ�
�ڵ�![]() ����
����![]() ��ֱ��
��ֱ��![]() �ϣ�
�ϣ�
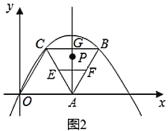
��3����![]() ��ֵ��Сʱ�����
��ֵ��Сʱ�����![]() ������Ϊ____________��
������Ϊ____________��
��4���ڣ�3���������£�����![]() ��
��![]() ��
��![]() ��
��![]() ���������������Ƿ���ڵ�
���������������Ƿ���ڵ�![]() ��ʹ����
��ʹ����![]() ��
��![]() ��
��![]() �������������
Ϊ�������������![]() ���ƣ������ڣ��������
���ƣ������ڣ��������![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
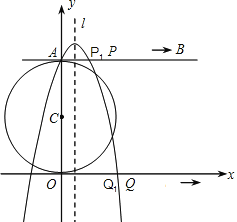
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��Ե�C(0��4)ΪԲ�ģ��뾶Ϊ4��Բ��y���������ڵ�A��AB�ǡ�C�����ߣ�����P�ӵ�A��ʼ��AB������ÿ��1����λ���ȵ��ٶ��˶�����Q��O�㿪ʼ��x����������ÿ��4����λ���ȵ��ٶ��˶����Ҷ���P��Q�ӵ�A�͵�Oͬʱ���������˶�ʱ��Ϊt(��)��
��1����t��1ʱ���õ�P1��Q1����A��P1��Q1����������߽���ʽ���Գ���l��
��2����tΪ��ֵʱ��ֱ��PQ���C���У���д����ʱ��P�͵�Q�����ꣻ
��3����(2)�������£������߶Գ���l�ϴ���һ��N��ʹNP��NQ��С�������N�����겢˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
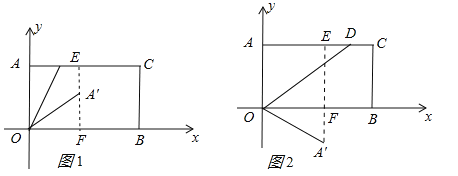
����Ŀ����2017����ʡ����12�⣬3�֣���֪��A��0��4����B��7��0����C��7��4��������AC��BC�õ�����AOBC����D�ı�AC�ϣ�����OA��OD�۵�����A�Ķ�Ӧ��ΪA'������A'�����νϳ����Աߵľ���֮��Ϊ1��3�����A'������Ϊ______________________________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ˮ��ɽ���ǽ�ɽ��ɽ�����������������ǵ��ճ������У���ˣ�Խ��Խ�����ϲ�������г����У�ij���г���������ij�ͺ����г�ʱ���Ը߳����۵�50%��ۣ���֪����۾������۸��ͺ����г�8���뽫���ֱ��100Ԫ����7��������ͬ��
��1������ͺ����г��Ľ��ۺͱ�۷ֱ��Ƕ���Ԫ��
��2�������ͺ����г��Ľ��۲��䣬����1���еı�۳��ۣ��õ�ƽ��ÿ�¿��۳�51������ÿ�����г�ÿ����20Ԫ��ÿ�¿ɶ��۳�3��������ͺ����г����۶���Ԫʱ��ÿ�»��������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�ڼ䣬ij�̳��ƻ������ס���������Ʒ����֪��������Ʒ1��������Ʒ3������240Ԫ����������Ʒ2��������Ʒ1������130Ԫ��
��1����ס���������Ʒÿ���Ľ��۷ֱ��Ƕ���Ԫ��
��2���̳���������Ʒ��ÿ��40Ԫ���ۣ�����Ʒ��ÿ��90Ԫ���ۣ�Ϊ�����г������蹺���ס���������Ʒ��100�����Ҽ�����Ʒ������������������Ʒ������4������������������Ľ�����������ȷ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ![]() ��һö�ʵؾ��ȵ������������ӣ������ĸ��沢�ֱ��������
��һö�ʵؾ��ȵ������������ӣ������ĸ��沢�ֱ��������![]() ��
��![]() ��
��![]() ��
��![]() ����ͼ
����ͼ![]() ��������
��������![]() ���㴦����һ��Ȧ����Ȧ��Ϸ�Ĺ���Ϊ����Ϸ��ÿ��һ�����ӣ������ŵ�һ���ϵ������Ǽ������������εı�˳ʱ�뷽�������������߳����磺����ͼ
���㴦����һ��Ȧ����Ȧ��Ϸ�Ĺ���Ϊ����Ϸ��ÿ��һ�����ӣ������ŵ�һ���ϵ������Ǽ������������εı�˳ʱ�뷽�������������߳����磺����ͼ![]() ��������һ������
��������һ������![]() ����˳ʱ��������
����˳ʱ��������![]() ���߳����䵽Ȧ
���߳����䵽Ȧ![]() �����ڶ�������
�����ڶ�������![]() ���ʹ�
���ʹ�![]() ��ʼ˳ʱ��������
��ʼ˳ʱ��������![]() ���߳����䵽Ȧ
���߳����䵽Ȧ![]() ��
��![]() ����Ϸ�ߴ�Ȧ
����Ϸ�ߴ�Ȧ![]() ������
������
��![]() ���μ������һ�����ӣ�����ص�Ȧ
���μ������һ�����ӣ�����ص�Ȧ![]() �ĸ���
�ĸ���![]() ��
��
��![]() ����������������ӣ����б����������ص�Ȧ
����������������ӣ����б����������ص�Ȧ![]() �ĸ���
�ĸ���![]() ����ָ������μ���ص�Ȧ
����ָ������μ���ص�Ȧ![]() �Ŀ�����һ����
�Ŀ�����һ����

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com