
【题目】(Ⅰ)如图1,在菱形![]() 中,已知
中,已知![]() ,
,![]() ,抛物线
,抛物线![]() (
(![]() )经过
)经过![]() ,
,![]() ,
,![]() 三点.
三点.
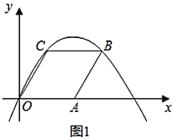
(1)点![]() 的坐标为__________,点
的坐标为__________,点![]() 的坐标为__________;
的坐标为__________;
(2)求抛物线的解析式.
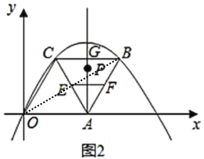
(Ⅱ)如图2,点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 的中点,直线
的中点,直线![]() 垂直
垂直![]() 于点
于点![]() ,点
,点![]() 在直线
在直线![]() 上.
上.
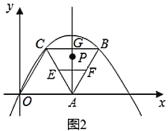
(3)当![]() 的值最小时,则点
的值最小时,则点![]() 的坐标为____________;
的坐标为____________;
(4)在(3)的条件下,连接![]() 、
、![]() 、
、![]() 得
得![]() ,问在抛物线上是否存在点
,问在抛物线上是否存在点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,请求出点
相似?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(Ⅰ)(1)![]() ,
, ![]() ;(Ⅰ)(2)
;(Ⅰ)(2)![]() ;(Ⅱ)(3)
;(Ⅱ)(3)![]() ;(Ⅱ)(4),存在,M点的坐标为
;(Ⅱ)(4),存在,M点的坐标为![]() 、
、![]() 、
、![]()
【解析】
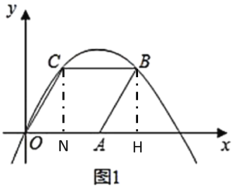
(Ⅰ)(1)过点B和点C分别是x轴的垂线于H和N,结合菱形的性质和![]() ,
,![]() ,即可求出AH,和BH及ON的长度,B点和C点坐标即可得出;
,即可求出AH,和BH及ON的长度,B点和C点坐标即可得出;
(Ⅰ)(2)把![]() ,
,![]() ,
,![]() 三点坐标代入抛物线
三点坐标代入抛物线![]() ,即可求得;
,即可求得;
(Ⅱ)(3)由题意知AG即为抛物线的对称轴,C点的对称点为B,连接OB,(见详解图),OB与AG的交点即为P点,![]() 的最小值即为OB长度,求出OB的直线解析式,即可求出P点坐标;
的最小值即为OB长度,求出OB的直线解析式,即可求出P点坐标;
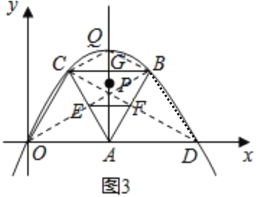
(Ⅱ)(4)由题意可知PE=PF,EF∥BC∥OD,进一步可知△PEF是底角为30°,顶角为120°的等腰三角形,设AG与抛物线交点为Q点(即为顶点),D点为O点关于对称轴的对称点,连接OB,CD,CQ,BQ,BD,再结合菱形中∠OCB=120°角,可知点O、点Q和点D即为所求M点。
(Ⅰ)(1)过点B和点C分别是x轴的垂线于H和N,
∵![]() ,
,![]() ,结合菱形的性质,
,结合菱形的性质,
∴![]() ,
,![]() ,
,
∴B点坐标为![]() ,C点坐标为
,C点坐标为![]() ,
,
故答案为:![]() ,
, ![]() ;
;
(Ⅰ)(2)将O点坐标![]() ,B点
,B点![]() ,C点坐标
,C点坐标![]() 三点坐标代入抛物线
三点坐标代入抛物线![]() ,可得:
,可得:
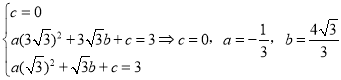
∴抛物线解析式为:![]()
(Ⅱ)(3)由题意知AG为抛物线的对称轴,C点的对称点为B,连接OB,OB与AG的交点即为P点,![]() 的最小值即为OB长度,
的最小值即为OB长度,
设OB直线为![]() ,将O点和B点坐标代入,求得:
,将O点和B点坐标代入,求得:![]() ,
,
令![]() ,y=2,
,y=2,
所以P点坐标为:![]()
(Ⅱ)(4)设AG与抛物线交点为Q点(即为顶点),D点为O点关于对称轴的对称点,连接OB,CD,CQ,BQ,BD,
∵点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 的中点
的中点
∴可知PE=PF,EF∥BC∥OD,
∴△PEF是底角为30°,顶角为120°的等腰三角形,
在△COB与△BCD中,OC=CB=BD,∠OCB=∠CBD=120°,
∴△COB≌△BCD∽△PEF
故O点(0,0)和D点![]() 即满足M点要求;
即满足M点要求;
另在△QCB中,∠QCB=∠BOD=30°,QC=QO,
∴△QCB∽△PEF,
故Q点![]() 也满足M点要求,
也满足M点要求,
故M点的坐标为:![]() 、
、![]() 、
、![]() .
.
故答案为:(Ⅰ)(1)![]() ,
, ![]() ;(Ⅰ)(2)
;(Ⅰ)(2)![]() ;(Ⅱ)(3)
;(Ⅱ)(3)![]() ;(Ⅱ)(4),存在,M点的坐标为
;(Ⅱ)(4),存在,M点的坐标为![]() 、
、![]() 、
、![]()


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】现有甲,乙两种机器人都被用来搬运某体育馆室内装潢材料甲型机器人比乙型机器人每小时少搬运30千克,甲型机器人搬运600千克所用的时间与乙型机器人搬运800千克所用的时间相同,两种机器人每小时分别搬运多少千克?设甲型机器人每小时搬运x千克,根据题意,可列方程为( )
A. ![]() =
=![]() B.
B. ![]() =
=![]()
C. ![]() =
=![]() D.
D. ![]() =
=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
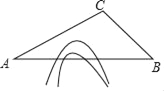
【题目】随着中国经济的快速发展以及科技水平的飞速提高,中国高铁正迅速崛起.高铁大大缩短了时空距离,改变了人们的出行方式.如图,A,B两地被大山阻隔,由A地到B地需要绕行C地,若打通穿山隧道,建成A,B两地的直达高铁,可以缩短从A地到B地的路程.已知:∠CAB=30°,∠CBA=45°,AC=640公里,求隧道打通后与打通前相比,从A地到B地的路程将约缩短多少公里?(参考数据:![]() ≈1.7,
≈1.7,![]() ≈1.4)
≈1.4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学活动小组在研究三角形拓展图形的性质时,经历了如下过程:
●操作发现
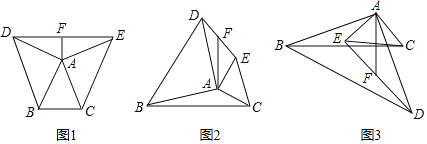
在等腰△ABC中,AB=AC,分别以AB和AC为腰,向△ABC的外侧作等腰直角三角形,如图①所示,连接DE,其中F是DE的中点,连接AF,则下列结论正确的是 (填序号即可)
①AF=![]() BC:②AF⊥BC;③整个图形是轴对称图形;④DE∥BC、
BC:②AF⊥BC;③整个图形是轴对称图形;④DE∥BC、
●数学思考
在任意△ABC中,分别以AB和AC为腰,向△ABC的外侧作等腰直角三角形,如图②所示,连接DE,其中F是DE的中点,连接AF,则AF和BC有怎样的数量和位置关系?请给出证明过程
●类比探索
在任意△ABC中,仍分别以AB和AC为腰,向△ABC的内侧作等腰直角三角形,如图③所示,连接DE,其中F是DE的中点,连接AF,试判断AF和BC的数量和位置关系是否发生改变?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李在学习了定理“直角三角形斜边上的中线等于斜边的一半”之后做了如下思考,请你帮他完成如下问题:
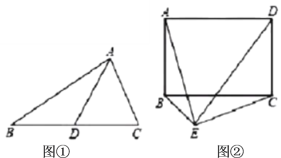
(1)他认为该定理有逆定理:“如果一个三角形某条边上的中线等于该边长的一半,那么这个三角形是直角三角形”应该成立.即如图①,在![]() 中,
中,![]() 是
是![]() 边上的中线,若
边上的中线,若![]() ,求证:
,求证:![]() .
.
(2)如图②,已知矩形![]() ,如果在矩形外存在一点
,如果在矩形外存在一点![]() ,使得
,使得![]() ,求证:
,求证:![]() .(可以直接用第(1)问的结论)
.(可以直接用第(1)问的结论)
(3)在第(2)问的条件下,如果![]() 恰好是等边三角形,请求出此时矩形的两条邻边
恰好是等边三角形,请求出此时矩形的两条邻边![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛. 赛后组委会整理参赛同学的成绩,并制作了如下不完整的频数分布表和频数分布直方图.
分数段(分数为x分) | 频数 | 百分比 |
60≤x<70 | 8 | 20% |
70≤x<80 | a | 30% |
80≤x<90 | 16 | b% |
90≤x<100 | 4 | 10% |
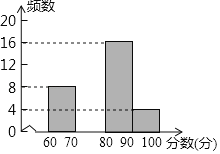
请根据图表提供的信息,解答下列问题:
(1)表中的a= ,b= ;请补全频数分布直方图;
(2)若用扇形统计图来描述成绩分布情况,则分数段70≤x<80对应扇形的圆心角的度数是 ;
(3)竞赛成绩不低于90分的4名同学中正好有2名男同学,2名女同学. 学校从这4名同学中随机抽2名同学接受电视台记者采访,则正好抽到一名男同学和一名女同学的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
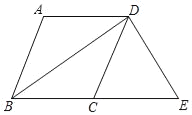
【题目】如图,在四边形ABCD中,AD∥BC,BA=BC,BD平分∠ABC.
(1)求证:四边形ABCD是菱形;
(2)过点D作DE⊥BD,交BC的延长线于点E,若BC=5,BD=8,求四边形ABED的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
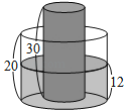
【题目】如图,有一内部装有水的直圆柱形水桶,桶高![]() ;另有一直圆柱形的实心铁柱,柱高
;另有一直圆柱形的实心铁柱,柱高![]() ,直立放置于水桶底面上,水桶内的水面高度为
,直立放置于水桶底面上,水桶内的水面高度为![]() ,且水桶与铁柱的底面半径比为
,且水桶与铁柱的底面半径比为![]() .今小贤将铁柱移至水桶外部,过程中水桶内的水量未改变,若不计水桶厚度,则水桶内的水面高度变为( )
.今小贤将铁柱移至水桶外部,过程中水桶内的水量未改变,若不计水桶厚度,则水桶内的水面高度变为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com