
【题目】某数学活动小组在研究三角形拓展图形的性质时,经历了如下过程:
●操作发现
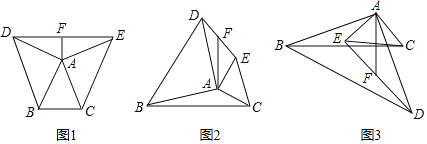
在等腰△ABC中,AB=AC,分别以AB和AC为腰,向△ABC的外侧作等腰直角三角形,如图①所示,连接DE,其中F是DE的中点,连接AF,则下列结论正确的是 (填序号即可)
①AF=![]() BC:②AF⊥BC;③整个图形是轴对称图形;④DE∥BC、
BC:②AF⊥BC;③整个图形是轴对称图形;④DE∥BC、
●数学思考
在任意△ABC中,分别以AB和AC为腰,向△ABC的外侧作等腰直角三角形,如图②所示,连接DE,其中F是DE的中点,连接AF,则AF和BC有怎样的数量和位置关系?请给出证明过程
●类比探索
在任意△ABC中,仍分别以AB和AC为腰,向△ABC的内侧作等腰直角三角形,如图③所示,连接DE,其中F是DE的中点,连接AF,试判断AF和BC的数量和位置关系是否发生改变?并说明理由.
【答案】操作发现:①②③④;数学思考:AF=![]() BC,AF⊥BC,理由见解析;类比探索:AF和BC的数量和位置关系不发生改变,理由见解析
BC,AF⊥BC,理由见解析;类比探索:AF和BC的数量和位置关系不发生改变,理由见解析
【解析】
操作发现:
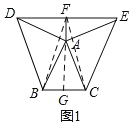
如图1,延长FA交BC于G,连接BF、CF.证明△FBA≌△FCA(SAS),得FB=FC,根据线段垂直平分线的逆定理可得FG是BC的垂直平分线,得②正确;
证明∠AFD≌△BGA(AAS),则AF=BG![]() BC,得①正确;
BC,得①正确;
根据内错角相等两直线平行,得④正确;
根据前面的证明可以得出整个图形是轴对称图形,故③正确,数学思考:
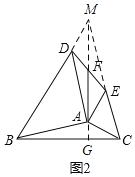
结论:AF![]() BC,AF⊥BC,如图2,作辅助线,构建平行四边形和三角形全等,证明四边形DAEM是平行四边形,得AD=EM=AB,AD∥EM,再证明△CAB≌△AEM(SAS),可得结论;
BC,AF⊥BC,如图2,作辅助线,构建平行四边形和三角形全等,证明四边形DAEM是平行四边形,得AD=EM=AB,AD∥EM,再证明△CAB≌△AEM(SAS),可得结论;
类比探索:
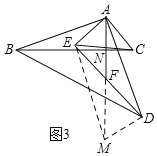
同理作辅助线,构建平行四边形和全等三角形,同理可得结论.
操作发现:
如图1,延长FA交BC于G.
∵△ABD和△ACE是等腰直角三角形,且∠BAD=∠CAE=90°,∴AB=AD,AC=AE.
∵AB=AC,∴AD=AE.
∵F是DE的中点,∴AF⊥DE,∠DAF=∠EAF,∴∠BAF=∠CAF.
∵AB=AC,AF=AF,∴△FBA≌△FCA(SAS),∴FB=FC,∴FG是BC的垂直平分线,即FG⊥BC,AF⊥BC,故②正确;
∵∠AGB=∠AFD=90°,∠BAG=∠FDA,∴∠AFD≌△BGA(AAS),∴AF=BG![]() BC,故①正确;
BC,故①正确;
∵∠AFD=∠AGC=90°,∴DE∥BC,故④正确;
根据前面的证明可以得出将图形1,沿FG对折左右两部分能完全重合,∴整个图形是轴对称图形,故③正确,结论正确的有:①②③④.
故答案为:①②③④;
数学思考:
结论:AF![]() BC,AF⊥BC,理由是:
BC,AF⊥BC,理由是:
如图2,延长AF至M,使FM=AF,连接DM、EM,延长FA交BC于G.
∵DF=EF,∴四边形DAEM是平行四边形,∴AD=EM=AB,AD∥EM,∴∠DAE+∠AEM=∠DAE+∠BAC=180°,∴∠BAC=∠AEM.
∵AC=AE,∴△CAB≌△AEM(SAS),∴AM=BC=2AF,∠AME=∠CBA,即AF![]() BC.
BC.
∵AD∥EM,∴∠DAM=∠AME=∠CBA.
∵∠BAD=90°,∴∠DAM+∠BAG=90°,∴∠CBA+∠BAG=∠AGB=90°,∴AF⊥BC;
类比探索:
AF和BC的数量和位置关系不发生改变,理由是:
如图3,延长AF至M,使AF=FM,连接EM、DM,设AF交BC于N.
∵EF=DF,∴四边形AEMD是平行四边形,∴AE=DM=AC.
∵∠BAD+∠EAC=180°,∴∠BAC+∠EAD=180°.
∵AE∥DM,∴∠ADM+∠EAD=180°,∴∠ADM=∠BAC.
∵AB=AD,∴△ABC≌△DAM(SAS),∴AM=BC=2AF,∠DAM=∠ABC,∴AF![]() BC.
BC.
∵∠DAM+∠BAF=∠ABC+∠BAF=90°,∴∠ANB=90°,∴AF⊥BC.


 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
【题目】如图,点E为矩形ABCD的边AD上一点,点P从点B出发沿BE→ED→DC运动到点C停止,点Q从点B出发沿BC运动到点C停止,它们运动的速度都是1cm/s.点P、Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2),已知y与t之间的函数图象如图2所示,给出下列结论:①当0<t≤10时,△BPQ是等腰三角形;②S△ABE=24cm2;③当14<t<22时,y=100﹣6t;④在运动过程中,使得△ABP是等腰三角形的P点一共3个;⑤当△BPQ与△BEA相似时,t=14.5,其中正确结论的序号是______.
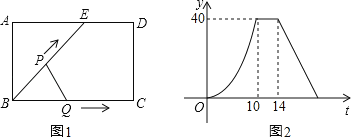
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABC中,AC=BC,过C作CD//AB.若AD平分∠CAB,则下列说法错误的是( )
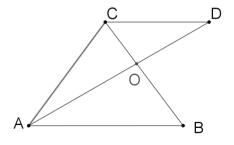
A. BC=CD
B. BO:OC=AB:BC
C. △CDO≌△BAO
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果基地为了选出适应市场需求的小西红柿秧苗,在条件基本相同的情况下,把两个品种的小西红柿秧苗各300株分别种植在甲、乙两个大棚,对市场最为关注的产量和产量的稳定性进行了抽样调查,过程如下:
收集数据从甲、乙两个大棚中分别随机收集了相同生产周期内25株秧苗生长出的小西红柿的个数:
甲:26,32,40,51,44,74,44,63,73,74,81,54,62,41,33,54,43,34,51,63,64,73,64,54,33
乙:27,35,46,55,48,36,47,68,82,48,57,66,75,27,36,57,57,66,58,61,71,38,47,46,71
整理数据按如下分组整理样本数据:
个数(x) 株数(株) 大棚 | 25≤x<35 | 35≤x<45 | 45≤x<55 | 55≤x<65 | 65≤x<75 | 75≤x<85 |
甲 | 5 |
| 5 |
| 4 | 1 |
乙 | 2 | 4 |
| 6 | 5 | 2 |
(说明:45个以下为产量不合格,45个及以上为产量合格,其中45≤x<65个为产量良好,65≤x<85个为产量优秀)
分析数据两组样本数据的平均数、众数和方差如下表所示:
大棚 | 平均数 | 众数 | 方差 |
甲 | 53 |
| 236.24 |
乙 | 53 | 57 | 215.04 |
得出结论
(1)补全上述表格;
(2)可以推断出 大棚的小西红柿秩苗品种更适应市场需求,理由为 (至少从两个不同的角度说明推断的合理性);
(3)估计乙大棚的300株小西红柿秧苗中产量优秀的有多少株?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对某一个函数给出如下定义:若存在实数![]() ,对于函数图象上横坐标之差为1的任意两点
,对于函数图象上横坐标之差为1的任意两点![]() ,
,![]() ,
,![]() 都成立,则称这个函数是限减函数,在所有满足条件的
都成立,则称这个函数是限减函数,在所有满足条件的![]() 中,其最大值称为这个函数的限减系数.例如,函数
中,其最大值称为这个函数的限减系数.例如,函数![]() ,当
,当![]() 取值
取值![]() 和
和![]() 时,函数值分别为
时,函数值分别为![]() ,
,![]() ,故
,故![]() ,因此函数
,因此函数![]() 是限减函数,它的限减系数为
是限减函数,它的限减系数为![]() .
.
(1)写出函数![]() 的限减系数;
的限减系数;
(2)![]() ,已知
,已知![]() (
(![]() )是限减函数,且限减系数
)是限减函数,且限减系数![]() ,求
,求![]() 的取值范围.
的取值范围.
(3)已知函数![]() 的图象上一点
的图象上一点![]() ,过点
,过点![]() 作直线
作直线![]() 垂直于
垂直于![]() 轴,将函数
轴,将函数![]() 的图象在点
的图象在点![]() 右侧的部分关于直线
右侧的部分关于直线![]() 翻折,其余部分保持不变,得到一个新函数的图象,如果这个新函数是限减函数,且限减系数
翻折,其余部分保持不变,得到一个新函数的图象,如果这个新函数是限减函数,且限减系数![]() ,直接写出
,直接写出![]() 点横坐标
点横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(Ⅰ)如图1,在菱形![]() 中,已知
中,已知![]() ,
,![]() ,抛物线
,抛物线![]() (
(![]() )经过
)经过![]() ,
,![]() ,
,![]() 三点.
三点.
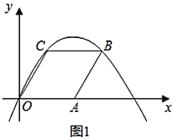
(1)点![]() 的坐标为__________,点
的坐标为__________,点![]() 的坐标为__________;
的坐标为__________;
(2)求抛物线的解析式.
(Ⅱ)如图2,点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 的中点,直线
的中点,直线![]() 垂直
垂直![]() 于点
于点![]() ,点
,点![]() 在直线
在直线![]() 上.
上.
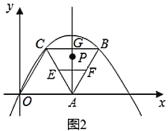
(3)当![]() 的值最小时,则点
的值最小时,则点![]() 的坐标为____________;
的坐标为____________;
(4)在(3)的条件下,连接![]() 、
、![]() 、
、![]() 得
得![]() ,问在抛物线上是否存在点
,问在抛物线上是否存在点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,请求出点
相似?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
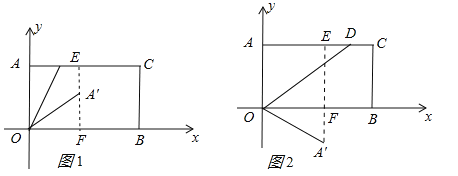
【题目】(2017江西省,第12题,3分)已知点A(0,4),B(7,0),C(7,4),连接AC,BC得到矩形AOBC,点D的边AC上,将边OA沿OD折叠,点A的对应边为A'.若点A'到矩形较长两对边的距离之比为1:3,则点A'的坐标为______________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
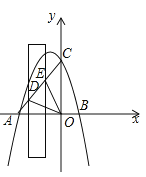
【题目】如图,抛物线![]() 与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,连结AC,现有一宽度为1,且长与y轴平行的矩形沿x轴方向平移,交直线AC于点D和E,△ODE周长的最小值为( )
与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,连结AC,现有一宽度为1,且长与y轴平行的矩形沿x轴方向平移,交直线AC于点D和E,△ODE周长的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com