
【题目】如图,点E为矩形ABCD的边AD上一点,点P从点B出发沿BE→ED→DC运动到点C停止,点Q从点B出发沿BC运动到点C停止,它们运动的速度都是1cm/s.点P、Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2),已知y与t之间的函数图象如图2所示,给出下列结论:①当0<t≤10时,△BPQ是等腰三角形;②S△ABE=24cm2;③当14<t<22时,y=100﹣6t;④在运动过程中,使得△ABP是等腰三角形的P点一共3个;⑤当△BPQ与△BEA相似时,t=14.5,其中正确结论的序号是______.
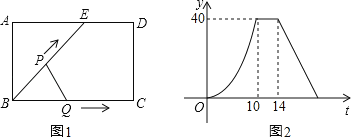
【答案】①②⑤
【解析】
①由图象可知,点Q到达C时,点P到E则BE=BC=10,ED=4,当0<t≤10时,BP始终等于BQ即可得出结论;
②由△BPQ的面积等于40求出DC的长,再由S△ABE=![]() ×ABAE即可得出结论;
×ABAE即可得出结论;
③当14<t<22时,由y=![]() BCPC代入即可得出结论;
BCPC代入即可得出结论;
④△ABP为等腰三角形需要分类讨论:当AB=AP时,ED上存在一个符合题意的P点,当BA=BP时,BE上存在一个符合题意的P点,当PA=PB时,点P在AB垂直平分线上,所以BE和CD上各存在一个符合题意的P点,即可得出结论;
⑤由当![]() 或
或![]() 时,△BPQ与△BEA相似,分别将数值代入即可得出结论.
时,△BPQ与△BEA相似,分别将数值代入即可得出结论.
解:①由图象可知,点Q到达C时,点P到E则BE=BC=10,ED=4,
∵它们运动的速度都是1cm/s.点P、Q同时开始运动,
∴当0<t≤10时,BP始终等于BQ,
∴△BPQ是等腰三角形;
故①正确;
②∵ED=4,BC=10,
∴AE=10﹣4=6
t=10时,△BPQ的面积等于 ![]() BCDC=
BCDC=![]() ×10×DC=40
×10×DC=40
∴AB=DC=8
∴S△ABE=![]() ×ABAE=
×ABAE=![]() ×8×6=24;
×8×6=24;
故②正确;
③当14<t<22时,y=![]() BCPC=
BCPC=![]() ×10×(22﹣t)=110﹣5t
×10×(22﹣t)=110﹣5t
故③错误;
④△ABP为等腰三角形需要分类讨论:
当AB=AP时,ED上存在一个符合题意的P点,
当BA=BP时,BE上存在一个符合题意的P点,
当PA=PB时,点P在AB垂直平分线上,所以BE和CD上各存在一个符合题意的P点,
∴共有4个点满足题意;
故④错误;
⑤∵△BEA为直角三角形,
∴只有点P在DC边上时,有△BPQ与△BEA相似,
由已知,PQ=22﹣t,
∴当![]() =
=![]() 或
或![]() =
=![]() 时,△BPQ与△BEA相似,
时,△BPQ与△BEA相似,
分别将数值代入![]() =
=![]() 或
或![]() =
=![]()
解得:t=![]() (不合题意舍去)或t=14.5;
(不合题意舍去)或t=14.5;
故⑤正确;
综上所述,正确的结论的序号是①②⑤.
故答案为:①②⑤.


科目:初中数学 来源: 题型:
【题目】已知y关于x的函数表达式是![]() ,下列结论不正确的是( )
,下列结论不正确的是( )
A.若![]() ,函数的最大值是5
,函数的最大值是5
B.若![]() ,当
,当![]() 时,y随x的增大而增大
时,y随x的增大而增大
C.无论a为何值时,函数图象一定经过点![]()
D.无论a为何值时,函数图象与x轴都有两个交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的图形P和直线AB,给出如下定义:M为图形P上任意一点,N为直线AB上任意一点,如果M,N两点间的距离有最小值,那么称这个最小值为图形P和直线AB之间的“确定距离”,记作d(P,直线AB).
已知A(2,0),B(0,2).
(1)求d(点O,直线AB);
(2)⊙T的圆心为![]() 半径为1,若d(⊙T,直线AB)≤1,直接写出t的取值范围;
半径为1,若d(⊙T,直线AB)≤1,直接写出t的取值范围;
(3)记函数![]() 的图象为图形Q.若d(Q,直线AB)=1,直接写出k的值.
的图象为图形Q.若d(Q,直线AB)=1,直接写出k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于图形
中,对于图形![]() ,若存在一个正方形
,若存在一个正方形![]() ,这个正方形的某条边与
,这个正方形的某条边与![]() 轴垂直,且图形
轴垂直,且图形![]() 上的所有的点都在该正方形的内部或者边上,则称该正方形
上的所有的点都在该正方形的内部或者边上,则称该正方形![]() 为图形
为图形![]() 的一个正覆盖.很显然,如果图形
的一个正覆盖.很显然,如果图形![]() 存在一个正覆盖,则它的正覆盖有无数个,我们将图形
存在一个正覆盖,则它的正覆盖有无数个,我们将图形![]() 的所有正覆盖中边长最小的一个,称为它的紧覆盖,如图所示,图形
的所有正覆盖中边长最小的一个,称为它的紧覆盖,如图所示,图形![]() 为三条线段和一个圆弧组成的封闭图形,图中的三个正方形均为图形
为三条线段和一个圆弧组成的封闭图形,图中的三个正方形均为图形![]() 的正覆盖,其中正方形
的正覆盖,其中正方形![]() 就是图形
就是图形![]() 的紧覆盖.
的紧覆盖.
(1)对于半径为2的![]() ,它的紧覆盖的边长为____.
,它的紧覆盖的边长为____.
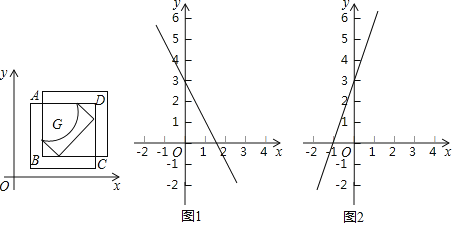
(2)如图1,点![]() 为直线
为直线![]() 上一动点,若线段
上一动点,若线段![]() 的紧覆盖的边长为
的紧覆盖的边长为![]() ,求点
,求点![]() 的坐标.
的坐标.
(3)如图2,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]()
①以![]() 为圆心,
为圆心,![]() 为半径的
为半径的![]() 与线段
与线段![]() 有公共点,且由
有公共点,且由![]() 与线段
与线段![]() 组成的图形
组成的图形![]() 的紧覆益的边长小于
的紧覆益的边长小于![]() ,直接写出
,直接写出![]() 的取值范围;
的取值范围;
②若在抛物线![]() 上存在点
上存在点![]() ,使得
,使得![]() 的紧覆益的边长为
的紧覆益的边长为![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接2022年冬奥会,鼓励更多的学生参与到志愿服务中来,甲、乙两所学校组织了志愿服务团队选拔活动,经过初选,两所学校各有400名学生进入综合素质展示环节.为了了解两所学校这些学生的整体情况,从两校进人综合素质展示环节的学生中分别随机抽取了50名学生的综合素质展示成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.
a.甲学校学生成绩的频数分布直方图如下(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);
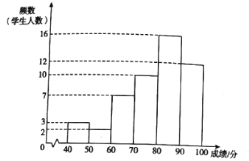
b.甲学校学生成绩在![]() 这一组的是:
这一组的是:
80 80 81 81.5 82 83 83 84
85 86 86.5 87 88 88.5 89 89
c.乙学校学生成绩的平均数、中位数、众数、优秀率(85分及以上为优秀)如下:
平均数 | 中位数 | 众数 | 优秀率 |
83.3 | 84 | 78 | 46% |
根据以上信息,回答下列问题:
(1)甲学校学生A,乙学校学生B的综合素质展示成绩同为83分,这两人在本校学生中的综合素质展示排名更靠前的是______(填“A”或“B”);
(2)根据上述信息,推断_____学校综合素质展示的水平更高,理由为_____(至少从两个不同的角度说明推断的合理性);
(3)若每所学校综合素质展示的前120名学生将被选入志愿服务团队,预估甲学校分数至少达到____分的学生才可以入选.
查看答案和解析>>
科目:初中数学 来源: 题型:
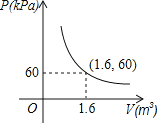
【题目】嵊州市三江购物中心为了迎接店庆,准备了某种气球,这些气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如下图所示.
(1)试写出这个函数的表达式;
(2)当气球的体积为2m3时,气球内气体的气压是多少?
(3)当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,对气球的体积有什么要求?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有甲,乙两种机器人都被用来搬运某体育馆室内装潢材料甲型机器人比乙型机器人每小时少搬运30千克,甲型机器人搬运600千克所用的时间与乙型机器人搬运800千克所用的时间相同,两种机器人每小时分别搬运多少千克?设甲型机器人每小时搬运x千克,根据题意,可列方程为( )
A. ![]() =
=![]() B.
B. ![]() =
=![]()
C. ![]() =
=![]() D.
D. ![]() =
=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=-![]() x2+
x2+![]() x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C:连接BC,点P为线段BC上方抛物线上的一动点,连接OP交BC于点Q.
x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C:连接BC,点P为线段BC上方抛物线上的一动点,连接OP交BC于点Q.
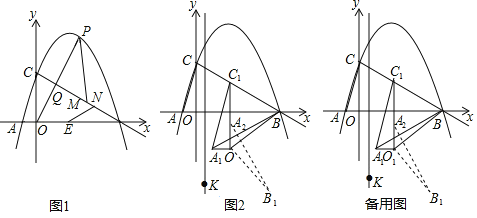
(1)如图1,当![]() 值最大时,点E为线段AB上一点,在线段BC上有两动点M,N(M在N上方),且MN=1,求PM+MN+NE-
值最大时,点E为线段AB上一点,在线段BC上有两动点M,N(M在N上方),且MN=1,求PM+MN+NE-![]() BE的最小值;
BE的最小值;
(2)如图2,连接AC,将△AOC沿射线CB方向平移,点A,C,O平移后的对应点分别记作A1,C1,O1,当C1B=O1B时,连接A1B、O1B,将△A1O1B绕点O1沿顺时针方向旋转90°后得△A2O1B1在直线x=![]() 上是否存在点K,使得△A2B1K为等腰三角形?若存在,直接写出点K的坐标;不存在,请说明理由.
上是否存在点K,使得△A2B1K为等腰三角形?若存在,直接写出点K的坐标;不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学活动小组在研究三角形拓展图形的性质时,经历了如下过程:
●操作发现
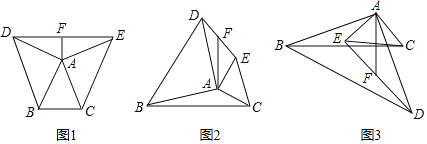
在等腰△ABC中,AB=AC,分别以AB和AC为腰,向△ABC的外侧作等腰直角三角形,如图①所示,连接DE,其中F是DE的中点,连接AF,则下列结论正确的是 (填序号即可)
①AF=![]() BC:②AF⊥BC;③整个图形是轴对称图形;④DE∥BC、
BC:②AF⊥BC;③整个图形是轴对称图形;④DE∥BC、
●数学思考
在任意△ABC中,分别以AB和AC为腰,向△ABC的外侧作等腰直角三角形,如图②所示,连接DE,其中F是DE的中点,连接AF,则AF和BC有怎样的数量和位置关系?请给出证明过程
●类比探索
在任意△ABC中,仍分别以AB和AC为腰,向△ABC的内侧作等腰直角三角形,如图③所示,连接DE,其中F是DE的中点,连接AF,试判断AF和BC的数量和位置关系是否发生改变?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com