
【题目】在平面直角坐标系![]() 中,对于图形
中,对于图形![]() ,若存在一个正方形
,若存在一个正方形![]() ,这个正方形的某条边与
,这个正方形的某条边与![]() 轴垂直,且图形
轴垂直,且图形![]() 上的所有的点都在该正方形的内部或者边上,则称该正方形
上的所有的点都在该正方形的内部或者边上,则称该正方形![]() 为图形
为图形![]() 的一个正覆盖.很显然,如果图形
的一个正覆盖.很显然,如果图形![]() 存在一个正覆盖,则它的正覆盖有无数个,我们将图形
存在一个正覆盖,则它的正覆盖有无数个,我们将图形![]() 的所有正覆盖中边长最小的一个,称为它的紧覆盖,如图所示,图形
的所有正覆盖中边长最小的一个,称为它的紧覆盖,如图所示,图形![]() 为三条线段和一个圆弧组成的封闭图形,图中的三个正方形均为图形
为三条线段和一个圆弧组成的封闭图形,图中的三个正方形均为图形![]() 的正覆盖,其中正方形
的正覆盖,其中正方形![]() 就是图形
就是图形![]() 的紧覆盖.
的紧覆盖.
(1)对于半径为2的![]() ,它的紧覆盖的边长为____.
,它的紧覆盖的边长为____.
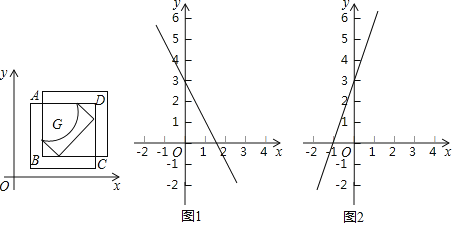
(2)如图1,点![]() 为直线
为直线![]() 上一动点,若线段
上一动点,若线段![]() 的紧覆盖的边长为
的紧覆盖的边长为![]() ,求点
,求点![]() 的坐标.
的坐标.
(3)如图2,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]()
①以![]() 为圆心,
为圆心,![]() 为半径的
为半径的![]() 与线段
与线段![]() 有公共点,且由
有公共点,且由![]() 与线段
与线段![]() 组成的图形
组成的图形![]() 的紧覆益的边长小于
的紧覆益的边长小于![]() ,直接写出
,直接写出![]() 的取值范围;
的取值范围;
②若在抛物线![]() 上存在点
上存在点![]() ,使得
,使得![]() 的紧覆益的边长为
的紧覆益的边长为![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)4;(2)(![]() ,2)或(2,-1);(3)①
,2)或(2,-1);(3)①![]() ≤r<1;②a≥
≤r<1;②a≥![]() 或a≤-2.
或a≤-2.
【解析】
(1)由题意半径为2的⊙O的外切正方形是半径为2的⊙O紧覆盖,由此即可解决问题;
(2)由题意当点P到坐标轴的距离等于2时,线段OP的紧覆盖的正方形的边长为2.分两种情形分别求解即可;
(3)①如图2中,作OH⊥AB于H.利用两种特殊位置解决问题即可;
②如图2-1中,由题意当抛物线与图中矩形EFGH区域有交点时,在抛物线y=ax2+2ax-2(a≠0)上存在点C,使得△ABC的紧覆益的边长为3;
(1)由题意半径为2的⊙O的外切正方形是半径为2的⊙O紧覆盖,
∴紧覆盖的边长为4,
故答案为4.
(2)由题意当点P到坐标轴的距离等于2时,线段OP的紧覆盖的边长为2.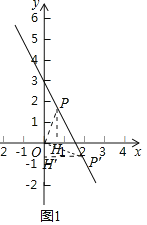
①当点P在第一象限时,作PH⊥x轴于H则PH=2,
y=2时,2=-2x+3,
x=![]() ,
,
∴P(![]() ,2).
,2).
②当点P′在第三象限时,作P′H′⊥y轴,则P′H′=2,
当x=2时,y=-1,
∴P′(2,-1).
综上所述,满足条件的点P坐标为(![]() ,2)或(2,-1).
,2)或(2,-1).
(3)①如图2中,作OH⊥AB于H.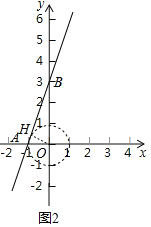
由题意A(-1,0),B(0,3),
∴OA=1,OB=3,AB=![]() ,
,
∵![]() OAOB=
OAOB=![]() ABOH,
ABOH,
∴OH=![]() ,
,
当⊙O经过点A时,r=1,此时由⊙O与线段AB组成的图形G的紧覆益的边长为4,
观察图象可知满足条件的r的范围为:![]() ≤r<1.
≤r<1.
②如图2-1中,如图由题意当抛物线与图中矩形EFGH区域有交点时,在抛物线y=ax2+2ax-2(a≠0)上存在点C,使得△ABC的紧覆益的边长为3.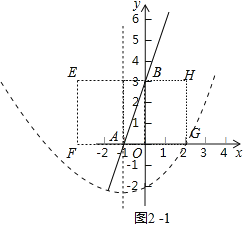
由题意E(-3,3),F(-3,0),G(2
当抛物线经过点G时,4a+4a-2=0,
∴a=![]() ,
,
∵抛物线的对称轴x=-1,经过(0,-2),
观察图象可知,当a≥![]() 时,在抛物线y=ax2+2ax-2(a≠0)上存在点C,使得△ABC的紧覆益的边长为3.
时,在抛物线y=ax2+2ax-2(a≠0)上存在点C,使得△ABC的紧覆益的边长为3.
当a<0时,抛物线经过点A时,解析式为y=-2(x+1)2,
观察图象可知,当a≤-2时,在抛物线y=ax2+2ax-2(a≠0)上存在点C,使得△ABC的紧覆益的边长为3.
综上所述,满足条件的a的值为a≥![]() 或a≤-2.
或a≤-2.


科目:初中数学 来源: 题型:
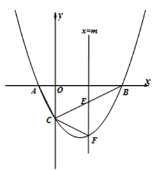
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于点C,已知A(–1,0),且直线BC的解析式为y=
与x轴交于A、B两点,与y轴交于点C,已知A(–1,0),且直线BC的解析式为y=![]() x-2,作垂直于x轴的直线
x-2,作垂直于x轴的直线![]() ,与抛物线交于点F,与线段BC交于点E(不与点B和点C重合).
,与抛物线交于点F,与线段BC交于点E(不与点B和点C重合).
(1)求抛物线的解析式;
(2)若△CEF是以CE为腰的等腰三角形,求m的值;
(3)点P为y轴左侧抛物线上的一点,过点P作![]() 交直线BC于点M,连接PB,若以P、M、B为顶点的三角形与△ABC相似,求P点的坐标.
交直线BC于点M,连接PB,若以P、M、B为顶点的三角形与△ABC相似,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图。

(1)这次被调查的同学共有 名;
(2)把条形统计图补充完整;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐。据此估算,该校18000名学生一餐浪费的食物可供多少人食用一餐?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() 反比例函数
反比例函数![]() 的图象经过点
的图象经过点![]() 且交
且交![]() 于点
于点![]() 过点
过点![]() 作
作![]() 轴于点
轴于点![]() .
.
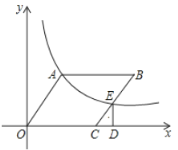
(1)求反比例函数的解析式;
(2)若点![]() 是反比例函数图象上一点,且
是反比例函数图象上一点,且![]() 的面积等于
的面积等于![]() 面积的
面积的![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
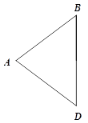
【题目】如图,在△ABD中,∠ABD = ∠ADB,分别以点B,D为圆心,AB长为半径在BD的右侧作弧,两弧交于点C,连接BC,DC和AC,AC与BD交于点O.
(1)用尺规补全图形,并证明四边形ABCD为菱形;
(2)如果AB = 5,![]() ,求BD的长.
,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知∠DAC=90°,△ABC是等边三角形,点P为射线AD上任意一点(点P与点A不重合),连结CP,将线段CP绕点C顺时针旋转60°得到线段CQ,连结QB并延长交直线AD于点E.
(1)如图1,猜想∠QEP= °;
(2)如图2,3,若当∠DAC是锐角或钝角时,其它条件不变,猜想∠QEP的度数,选取一种情况加以证明;
(3)如图3,若∠DAC=135°,∠ACP=15°,且AC=4,求BQ的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E为矩形ABCD的边AD上一点,点P从点B出发沿BE→ED→DC运动到点C停止,点Q从点B出发沿BC运动到点C停止,它们运动的速度都是1cm/s.点P、Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2),已知y与t之间的函数图象如图2所示,给出下列结论:①当0<t≤10时,△BPQ是等腰三角形;②S△ABE=24cm2;③当14<t<22时,y=100﹣6t;④在运动过程中,使得△ABP是等腰三角形的P点一共3个;⑤当△BPQ与△BEA相似时,t=14.5,其中正确结论的序号是______.
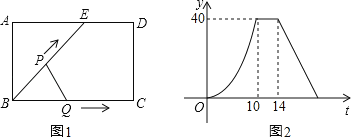
查看答案和解析>>
科目:初中数学 来源: 题型:
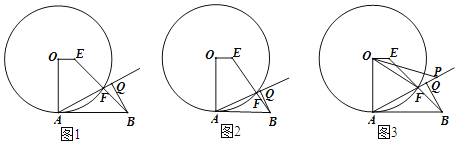
【题目】如图,OA是⊙O的半径,点E为圆内一点,且OA⊥OE,AB是⊙O的切线,EB交⊙O于点F,BQ⊥AF于点Q.
(1)如图1,求证:OE∥AB;
(2)如图2,若AB=AO,求![]() 的值;
的值;
(3)如图3,连接OF,∠EOF的平分线交射线AF于点P,若OA=2,cos∠PAB=![]() ,求OP的长.
,求OP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com