
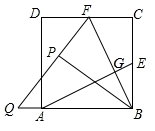
【题目】如图,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE、BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA的延长线于点Q,则下列结论:
①AE=BF;②S四边形ECFG=S△ABG;③△BFQ是等腰三角形;④![]() .
.
其中一定正确的个数是( )
A.1个B.2个C.3个D.4个
【答案】D
【解析】
①根据正方形的性质和已知条件证明△ABE≌△BCF即可;②根据三角形ABE和三角形BFC面积相等即可证明S四边形ECFG=S△ABG;③根据折叠可得∠CFB=∠PFB,由DC∥AB得∠CFB=∠FBA,等量代换后即可证明△BFQ是等腰三角形;④可以设正方形边长为1,AQ=x,AH=y,作FI⊥AB于点I,进而根据同角三角函数值相等用含x的式子表示y,然后求出QH,利用勾股定理列出方程求出x的值,即可得到![]() .
.
解:①∵在正方形ABCD中,E、F分别为BC、CD的中点,
∴AB=BC,∠ABE=∠BCF=90°,BE=CF,
∴△ABE≌△BCF(SAS),
∴AE=BF,故①正确;
②∵△ABE≌△BCF,
∴S△BCF=S△ABE,
∴SBCF﹣S△BGE=S△ABE﹣S△BGE,即S四边形ECFG=S△ABG,故②正确;
③∵由折叠可知:∠CFB=∠PFB,
∵DC∥AB,
∴∠CFB=∠FBA,
∴∠PFB=∠FBA,
∴QF=QB,
∴△BFQ是等腰三角形,故③正确;
④如图所示:
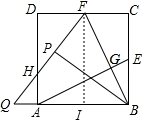
设PQ与AD交于点H,作FI⊥AB于点I,则四边形DAIF是矩形,
设正方形ABCD边长为1,AQ=x,AH=y,
则FI=AD=1,AI=![]() ,QI=x+
,QI=x+![]() ,
,
在Rt△AQH和Rt△FIQ中,tan∠Q=![]() ,即
,即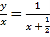 ,
,
∴y=![]() ,
,
∵AH∥FI,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
在Rt△AHQ中,根据勾股定理得:x2+y2=y2(1+x)2,
∴x2+(![]() )2=(
)2=(![]() )2(1+x)2,
)2(1+x)2,
解得:x=![]() ,
,
经检验,x=![]() 是方程的解,
是方程的解,
∴BQ![]() ,
,
∴![]() ,故④正确.
,故④正确.
∴正确的是①②③④,
故选:D.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx﹣3(a≠0)与x轴交于点A(﹣1,0)和点B,且OB=3OA,与y轴交于点C,此抛物线顶点为点D.
(1)求抛物线的表达式及点D的坐标;
(2)如果点E是y轴上的一点(点E与点C不重合),当BE⊥DE时,求点E的坐标;
(3)如果点F是抛物线上的一点.且∠FBD=135°,求点F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一项答题竞猜活动,在6个式样、大小都相同的箱子中有且只有一个箱子里藏有礼物.参与选手将回答5道题目,每答对一道题,主持人就从6个箱子中去掉一个空箱子.而选手一旦答错,即取消后面的答题资格,从剩下的箱子中选取一个箱子.
(1)一个选手答对了4道题,求他选中藏有礼物的箱子的概率;
(2)已知一个选手选中藏有礼物的箱子的概率为![]() ,则他答对了几道题?
,则他答对了几道题?
查看答案和解析>>
科目:初中数学 来源: 题型:
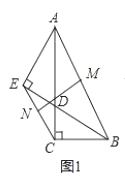
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,连接
上,连接![]() ,过
,过![]() 作
作![]() 的垂线交
的垂线交![]() 的延长线于点
的延长线于点![]() .
.
(1)若![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 的中点,如图1,求证:
的中点,如图1,求证:![]() ;
;
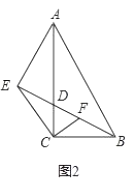
(2)如图2,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
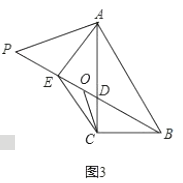
(3)如图3,以![]() 为一边作一个角等于
为一边作一个角等于![]() ,这个角的另一边与
,这个角的另一边与![]() 的延长线交于
的延长线交于![]() 点,
点,![]() 为
为![]() 的中点,连接
的中点,连接![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.
(1)求证:DH是圆O的切线;
(2)若A为EH的中点,求![]() 的值;
的值;
(3)若EA=EF=1,求圆O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
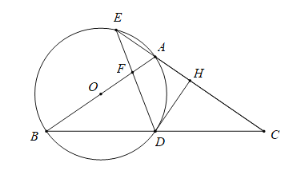
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径作圆
为直径作圆![]() ,分别交
,分别交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() 交线段
交线段![]() 于点
于点![]() .
.
(1)求证:![]() 是圆
是圆![]() 的切线;
的切线;
(2)若![]() 为
为![]() 的中点,求
的中点,求![]() 的值;
的值;
(3)若![]() ,求圆
,求圆![]() 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:[x]表示不大于x 的最整数,(x) 表示不小于x的最小整数,[x) 表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2,则下列说法正确的是__________(写出所有正确说法).
①当x=1.7时,[x]+(x)+[x)=6;
②当x=-2.1时,[x]+(x)+[x)=-7;
③方程4[x]+3(x)+[x)=11的解为1<x<1.5;
④当-1<x<1时, 函数y=[x]+(x)+x 的图像y=4x 的图像有两个交点.
【答案】②③
【解析】分析:(1)根据题目中给的计算方法代入计算后判定即可;(2)根据题目中给的计算方法代入计算后判定即可;(3)根据题目中给的计算方法代入计算后判定即可;(4)结合x的取值范围,分类讨论,利用题目中给出的方法计算后判定即可.
详解:
①当x=1.7时,
[x]+(x)+[x)
=[1.7]+(1.7)+[1.7)=1+2+2=5,故①错误;
②当x=﹣2.1时,
[x]+(x)+[x)
=[﹣2.1]+(﹣2.1)+[﹣2.1)
=(﹣3)+(﹣2)+(﹣2)=﹣7,故②正确;
③当1<x<1.5时,
4[x]+3(x)+[x)
=4×1+3×2+1
=4+6+1
=11,故③正确;
④∵﹣1<x<1时,
∴当﹣1<x<﹣0.5时,y=[x]+(x)+x=﹣1+0+x=x﹣1,
当﹣0.5<x<0时,y=[x]+(x)+x=﹣1+0+x=x﹣1,
当x=0时,y=[x]+(x)+x=0+0+0=0,
当0<x<0.5时,y=[x]+(x)+x=0+1+x=x+1,
当0.5<x<1时,y=[x]+(x)+x=0+1+x=x+1,
∵y=4x,则x﹣1=4x时,得x=![]() ;x+1=4x时,得x=
;x+1=4x时,得x=![]() ;当x=0时,y=4x=0,
;当x=0时,y=4x=0,
∴当﹣1<x<1时,函数y=[x]+(x)+x的图象与正比例函数y=4x的图象有三个交点,故④错误,
故答案为:②③.
点睛:本题是阅读理解题,前三问比较容易判定,根据题目所给的方法判定即可;第四问较难,结合x的取值范围分情况讨论即可.
【题型】填空题
【结束】
19
【题目】先化简再求值: ![]() ,其中
,其中![]() ,
, ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.Rt△ABC中,已知∠C=90°,∠B=50°,点D在边BC上,BD=2CD(图4).把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m=_________![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com