练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】一项答题竞猜活动，在6个式样、大小都相同的箱子中有且只有一个箱子里藏有礼物．参与选手将回答5道题目，每答对一道题，主持人就从6个箱子中去掉一个空箱子．而选手一旦答错，即取消后面的答题资格，从剩下的箱子中选取一个箱子．

    （1）一个选手答对了4道题，求他选中藏有礼物的箱子的概率；

    （2）已知一个选手选中藏有礼物的箱子的概率为，则他答对了几道题？

    【答案】（1）；（2）1道题.

    【解析】

    （1）求得剩下的箱子数，用概率公式求得概率即可；

    （2）根据概率求得箱子的总数，然后求得答对的题目即可．

    （1）∵共6个箱子，答对了4道取走4个箱子，

    ∴还剩2个箱子，

    ∴一个选手答对了4道题，求他选中藏有礼物的箱子的概率；

    （2）∵一个选手选中藏有礼物的箱子的概率为，

    ∴他从5个箱子中选择一个箱子，

    ∴则他答对了1道题；

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，函数和的图象分别为直线，，过点(1，0)作轴的垂线交于点，过点作轴的垂线交于点，过点作轴的垂线交于点，过点作轴的垂线交于点，…依次进行下去，则点的坐标为_________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

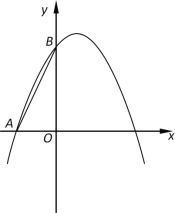
    【题目】如图，抛物线经过点A（﹣2，0），点B（0，4）.

    （1）求这条抛物线的表达式；

    （2）P是抛物线对称轴上的点，联结AB、PB，如果∠PBO=∠BAO，求点P的坐标；

    （3）将抛物线沿y轴向下平移m个单位，所得新抛物线与y轴交于点D，过点D作DE∥x轴交新抛物线于点E，射线EO交新抛物线于点F，如果EO=2OF，求m的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=-x2+2x+m+1交x轴于点A(a,0）和B(b,0），交y轴于点C，抛物线的顶点为D，下列四个判断：①当x>0时，y>0；②若a=-1，则b=3；③抛物线上有两点P(x1，y1）和Q（x2，y2），若x1<1<x2，且x1+x2>2，则y1>y2；④点C关于抛物线对称轴的对称点为E，点G、F分别在x轴和y轴上，当m=2时，四边形EDGF周长的最小值为，其中，判断正确的序号是（ ）

    A.①②B.②③C.①③D.②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

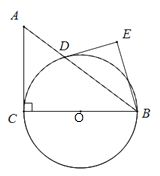
    【题目】如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，以边BC为直径作⊙O，交AB于D，DE是⊙O的切线，过点B作DE的垂线，垂足为E．

    (1)求证∠ABC＝∠ABE；

    (2)求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

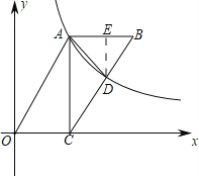
    【题目】如图，在OABC中C（2，0），AC⊥OC，反比例函数y=（k＞0）在第一象限内的图象过点A，且与BC交于点D，点D的横坐标为3，连接AD，△ABD的面积为，则k的值为（ ）

    A.4B.5C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线与x轴交于点A，B两点（点A在点B左边），与y轴交于点C．

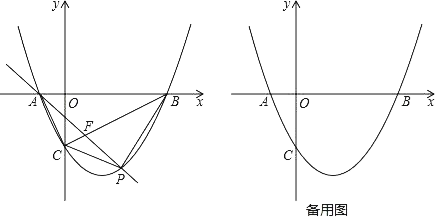
    （1）求A，B两点的坐标．

    （2）点P是线段BC下方的抛物线上的动点，连结PC，PB．

    ①是否存在一点P，使△PBC的面积最大，若存在，请求出△PBC的最大面积；若不存在，试说明理由．

    ②连结AC，AP，AP交BC于点F，当∠CAP＝∠ABC时，求直线AP的函数表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形ABCD中，E、F分别为BC、CD的中点，连接AE、BF交于点G，将△BCF沿BF对折，得到△BPF，延长FP交BA的延长线于点Q，则下列结论：

    ①AE=BF；②S四边形ECFG=S△ABG；③△BFQ是等腰三角形；④．

    其中一定正确的个数是（　　）

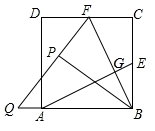
    A.1个B.2个C.3个D.4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】从三角形（不是等腰三角形）一个顶点引出一条射线于对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线．

    （1）如图1，在△ABC中，CD为角平分线，∠A=40°，∠B=60°，求证：CD为△ABC的完美分割线．

    （2）在△ABC中，∠A=48°，CD是△ABC的完美分割线，且△ACD为等腰三角形，求∠ACB的度数．

    （3）如图2，△ABC中，AC=2，BC=，CD是△ABC的完美分割线，且△ACD是以CD为底边的等腰三角形，求完美分割线CD的长．

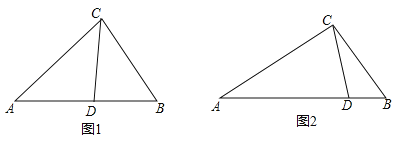
    查看答案和解析>>

    同步练习册答案