
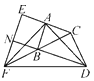
【题目】如图,在△ABC和△BCD中,∠BAC=∠BCD=90°,AB=AC,CB=CD.延长CA至点E,使AE=AC;延长CB至点F,使BF=BC.连接AD,AF,DF,EF.延长DB交EF于点N.
(1)求证:AD=AF;
(2)求证:BD=EF;
(3)试判断四边形ABNE的形状,并说明理由.

【答案】(1) (2)证明见解析;(3)四边形ABNE是正方形.理由见解析.
【解析】
(1)由等腰直角三角形的性质得出∠ABC=∠ACB=45°,求出∠ABF=135°,∠ABF=∠ACD,证出BF=CD,由SAS证明△ABF≌△ACD,即可得出AD=AF;
(2)由(1)知AF=AD,△ABF≌△ACD,得出∠FAB=∠DAC,证出∠EAF=∠BAD,由SAS证明△AEF≌△ABD,得出对应边相等即可;
(3)由全等三角形的性质得出得出∠AEF=∠ABD=90°,证出四边形ABNE是矩形,由AE=AB,即可得出四边形ABNE是正方形.
(1)证明:∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∴∠ABF=135°.
∵∠BCD=90°,
∴∠ACD=135°.
∴∠ABF=∠ACD.
∵CB=CD,CB=BF,
∴BF=CD.
在△ABF和△ACD中,
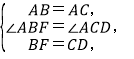
∴△ABF≌△ACD,
∴AD=AF;
(2)证明:由(1)知AF=AD,△ABF≌△ACD,
∴∠FAB=∠DAC.
∵∠BAC=90°,
∴∠EAB=∠BAC=90°,
∴∠EAF=∠BAD.
∵AB=AC,AC=AE,
∴AB=AE.
在△AEF和△ABD中,
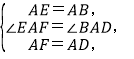
∴△AEF≌△ABD.
∴BD=EF.
(3)解:四边形ABNE是正方形.理由:
∵CD=CB,∠BCD=90°,
∴∠CBD=45°.
∵∠ABC=45°,
∴∠ABD=90°.
∴∠ABN=90°.
由(2)知∠EAB=90°,△AEF≌△ABD,
∴∠AEF=∠ABD=90°.
∴四边形ABNE是矩形.
又∵AE=AB,
∴矩形ABNE是正方形.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】学校的某社团组织了一次智力竞赛,共a、b、c三题,每题或者得满分或者得0分,其中题a满分10分,题b、题c满分均为15分.竞赛结果,每个学生至少答对了一题,三题全答对的有2人,答对其中两道题的有14人,答对题a的人数与答对题b的人数之和为29,答对题a的人数与答对题c的人数之和为27,答对题b的人数与答对题c的人数之和为20,则这个社团的平均成绩是_____分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某园林部门决定利用现有的349盆甲种花卉和295盆乙种花卉搭配A. B两种园艺造型共50个,摆放在迎宾大道两侧。已知搭配一个A种造型需甲种花卉8盆,乙种花卉4盆;搭配一个B种造型需甲种花卉5盆,乙种花卉9盆。
(1)某校九年级某班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮助设计出来;
(2)若搭配一个A种造型的成本是200元,搭配一个B种造型的成本是360元,试说明(1)中哪种方案成本最低,最低成本是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)定义:直角三角形两直角边的平方和等于斜边的平方。如:直角三角形的直角边分别为3、4,则斜边的平方=32+42=25.已知:Rt△ABC中,∠C=90°,AC=8,AB=10,直接写出BC2=___.

(2)应用:已知正方形ABCD的边长为4,点P为AD边上的一点,AP=![]() AD,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为多少?
AD,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:
①AE=CF;②△EPF是等腰直角三角形;③S四边形AEPF=![]() S△ABC;④EF=AP.上述结论始终正确的有( )
S△ABC;④EF=AP.上述结论始终正确的有( )
②③

A.①②③④B.①②③C.①③④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价分别为190元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1770元 |
第二周 | 4台 | 10台 | 3060 元 |
(进价、售价均保持不变,利润=销售收入一进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5300元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标,若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市救灾物资储备仓库共存储了A,B,C三类救灾物资,下面的统计图是三类物资存储量的不完整统计图.
(1)求A类物资的存储量,并将两个统计表补充完整;
(2)现计划租用甲、乙两种货车共8辆,一次性将A、B两类物资全部运往某灾区.已知甲种货车最多可装A类物资10吨和B类物资40吨,乙种货车最多可装A、B类物资各20吨,则物资储备仓库安排甲、乙两种货车有几种方案?请你帮助设计出来.

查看答案和解析>>
科目:初中数学 来源: 题型:
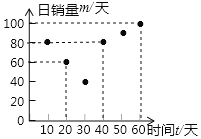
【题目】某公司生产某环保产品的成本为每件40元,经过市场调研发现:这件产品在未来两个月![]() 天
天![]() 的日销量
的日销量![]() 件
件![]() 与时间
与时间![]() 天
天![]() 的关系如图所示
的关系如图所示![]() 未来两个月
未来两个月![]() 天
天![]() 该商品每天的价格
该商品每天的价格![]() 元
元![]() 件
件![]() 与时间
与时间![]() 天
天![]() 的函数关系式为:
的函数关系式为: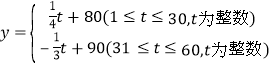
根据以上信息,解决以下问题:
![]() 请分别确定
请分别确定![]() 和
和![]() 时该产品的日销量
时该产品的日销量![]() 件
件![]() 与时间
与时间![]() 天
天![]() 之间的函数关系式;
之间的函数关系式;
![]() 请预测未来第一月日销量利润
请预测未来第一月日销量利润![]() 元
元![]() 的最小值是多少?第二个月日销量利润
的最小值是多少?第二个月日销量利润![]() 元
元![]() 的最大值是多少?
的最大值是多少?
![]() 为创建“两型社会”,政府决定大力扶持该环保产品的生产和销售,从第二个月开始每销售一件该产品就补贴a元
为创建“两型社会”,政府决定大力扶持该环保产品的生产和销售,从第二个月开始每销售一件该产品就补贴a元![]() 有了政府补贴以后,第二个月内该产品日销售利润
有了政府补贴以后,第二个月内该产品日销售利润![]() 元
元![]() 随时间
随时间![]() 天
天![]() 的增大而增大,求a的取值范围.
的增大而增大,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com