
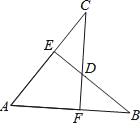
【题目】如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:
①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上;④点C在AB的中垂线上.
以上结论正确的有( )个.
A. 1 B. 2 C. 3 D. 4
 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的弦,半径OA=2,OA和AB的长度是关于x的一元二次方程x2﹣4x+a=0的两个实数根.
(1)求弦AB的长度;
(2)计算S△AOB;
(3)⊙O上一动点P从A点出发,沿逆时针方向运动一周,当S△POA=S△AOB时,求P点所经过的弧长(不考虑点P与点B重合的情形).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂生产的RGZ-120型体重秤,最大称重120千克,你在体检时可看到如图(1)所示的显示盘。已知指针顺时针旋转角x(度)与体重y(千克)有如下关系:
x(度) | 0 | 72 | 144 | 216 |
y(千克) | 0 | 25 | 50 | 75 |
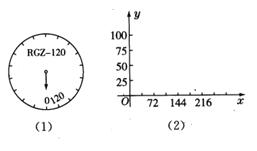
(1)根据表格中的数据在平面直角坐标系,图(2)中描出相应的点,顺次连接各点后,你发现这些点在哪一种函数的图象上?合情猜想符合这个图象的函数解析式;
(2)验证这些点的坐标是否满足函数解析式,归纳你的结论(写出自变量x的取值范围);
(3)当指针旋转到158.4度的位置时,显示盘上的体重读数模糊不清,用解析式求出此时的体重。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植-亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图1所示的一次函数关系.随着补贴数额x的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足如图2所示的一次函数关系.
(1)在政府未出台补贴措施前,该市种植这种蔬菜的总收益额为多少?
(2)分别求出政府补贴政策实施后,种植亩数y和每亩蔬菜的收益z与政府补贴数额x之间的函数关系式;
(3)要使全市这种蔬菜的总收益w(元)最大,政府应将每亩补贴数额x定为多少?并求出总收益w的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C、D在⊙O上,O点在∠D的内部,四边形OABC为平行四边形
(1)求∠D的度数;
(2)E、F分别是AB、BC上的两点,且AE=CF,延长OE、CB交于点G,求证:∠COF=∠CGO
(3)在第(2)小题的条件下,连接AC,交OE于点H,若OC=2,CF=1,求OH∶EH∶EG的值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+4与坐标轴分别交于点M、N.
x+4与坐标轴分别交于点M、N.
(1)求M,N两点的坐标;
(2)若点P在坐标轴上,且P到直线y=﹣![]() x+4的距离为
x+4的距离为![]() ,求符合条件的P点坐标.
,求符合条件的P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】班主任要从甲、乙两名跳远运动员中挑选一人参加校运动会比赛.在最近的10次选拔赛中,他们的成绩如下(单位:cm):
甲 | 585 | 596 | 610 | 598 | 612 | 597 | 604 | 600 | 613 | 601 |
乙 | 613 | 618 | 580 | 574 | 618 | 593 | 585 | 590 | 598 | 624 |
(1)他们的平均成绩分别是多少?
(2)甲、乙两名运动员这10次比赛成绩的极差、方差分别是多少?
(3)怎样评价这两名运动员的运动成绩?
(4)历届比赛表明,成绩达到5.96m就有可能夺冠,你认为为了夺冠应选择谁参加这项比赛?如果历届比赛成绩表明,成绩达到6.10m就能打破记录,那么你认为为了打破记录应选择谁参加这项比赛?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com