
【题目】如图,已知AB是⊙O的弦,半径OA=2,OA和AB的长度是关于x的一元二次方程x2﹣4x+a=0的两个实数根.
(1)求弦AB的长度;
(2)计算S△AOB;
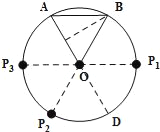
(3)⊙O上一动点P从A点出发,沿逆时针方向运动一周,当S△POA=S△AOB时,求P点所经过的弧长(不考虑点P与点B重合的情形).

【答案】(1)AB=2;(2)S△AOB=![]() ;(3)当S△POA=S△AOB时,P点所经过的弧长分别是
;(3)当S△POA=S△AOB时,P点所经过的弧长分别是![]() 、
、![]() 、
、![]() .
.
【解析】试题分析:(1)OA和AB的长度是一元二次方程的根,所以利用一元二次方程的根与系数的关系即可求出AB的长度;
(2)作出△AOB的高OC,然后求出OC的长度即可求出面积;
(3)由题意知:两三角形有公共的底边,要面积相等,即高要相等.
试题解析:(1)由题意知:OA和AB的长度是x2﹣4x+a=0的两个实数根,
∴OA+AB=﹣![]() =4,
=4,
∵OA=2,
∴AB=2;
(2)过点C作OC⊥AB于点C,
∵OA=AB=OB=2,∴△AOB是等边三角形,∴AC=![]() AB=1,
AB=1,
在Rt△ACO中,由勾股定理可得:OC=![]() ,∴S△AOB=
,∴S△AOB=![]() AB﹒OC=
AB﹒OC=![]() ×2×
×2×![]() =
=![]() ;
;
(3)延长AO交⊙O于点D,由于△AOB与△POA有公共边OA,
当S△POA=S△AOB时,∴△AOB与△POA高相等,
由(2)可知:等边△AOB的高为![]() ,∴点P到直线OA的距离为
,∴点P到直线OA的距离为![]() ,这样点共有3个
,这样点共有3个
①过点B作BP1∥OA交⊙O于点P1,∴∠BOP1=60°,
∴此时点P经过的弧长为: ![]() =
=![]() ,
,
②作点P2,使得P1与P2关于直线OA对称,∴∠P2OD=60°,
∴此时点P经过的弧长为: ![]() =
=![]() ,
,
③作点P3,使得B与P3关于直线OA对称,∴∠P3OP2=60°,
∴此时P经过的弧长为: ![]() =
=![]() ,
,
综上所述:当S△POA=S△AOB时,P点所经过的弧长分别是![]() 、
、![]() 、
、![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,ABC中,AB=AC=4![]() ,cosC=
,cosC=![]() .
.
(1)动手操作:利用尺规作以AC为直径的⊙O,并标出⊙O与AB的交点D,与BC的交点E(保留作图痕迹,不写作法).
(2)综合应用:在你所作的圆中,求证: ![]() ;
;
(3)求△BDE的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汛期来临,水库水位不断上涨,经勘测发现,水库现在超过警戒线水量640万米3,设水流入水库的速度是固定的,每个泄洪闸速度也是固定的,泄洪时,每小时流入水库的水量16万米3,每小时每个泄洪闸泄洪14万米3,已知泄洪的前a小时只打开了两个泄洪闸,水库超过警戒线的水量y(万米3)与泄洪时间s(小时)的关系如图所示,根据图象解答问题:

(1)求a的值;
(2)求泄洪20小时,水库现超过警戒线水量;
(3)若在开始泄洪后15小时内将水库降到警戒线水量,问泄洪一开始至少需要同时打开几个泄洪闸?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验与探究
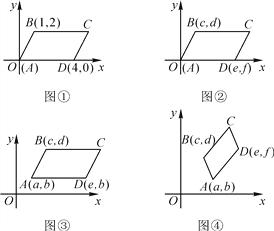
(1)在图①,图②,图③中,给出平行四边形ABCD的顶点A,B,D的坐标,写出图①,图②,图③中的顶点C的坐标,它们分别是________,___________,____________;
(2)在图④中,给出平行四边形ABCD的顶点A,B,D的坐标(如图所示),求出顶点C的坐标(C点坐标用含a,b,c,d,e,f的代数式表示);
归纳与发现
(3)通过对图①,图②,图③,图④的观察和顶点C的坐标的探究,你会发现:无论平行四边形ABCD处于直角坐标系中哪个位置,当其顶点C坐标为(m,n)(如图④)时,则四个顶点的横坐标a,c,m,e之间的等量关系为___________,纵坐标b,d,n,f之间的等量关系为__________.(不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD和正方形CEFG,连结AF交BC于点O,点P是AF的中点,过点P作PH⊥DG于H,CD=2,CG=1.
(1)如图1,点D、C、G在同一直线上,点E在BC边上,求PH的长;
(2)把正方形CEFG绕着点C逆时针旋转α(0°<α<180°)
①如图2,当点E落在AF上时,求CO的长;
②如图3,当DG=![]() 时,求PH的长.
时,求PH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
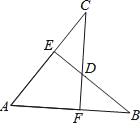
【题目】如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:
①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上;④点C在AB的中垂线上.
以上结论正确的有( )个.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com