
【题目】如图,ABC中,AB=AC=4![]() ,cosC=
,cosC=![]() .
.
(1)动手操作:利用尺规作以AC为直径的⊙O,并标出⊙O与AB的交点D,与BC的交点E(保留作图痕迹,不写作法).
(2)综合应用:在你所作的圆中,求证: ![]() ;
;
(3)求△BDE的周长.

【答案】(1)作图见解析;(2)证明见解析;(3)△BDE的周长为8+![]() .
.
【解析】试题分析:做AC的中垂线得出圆心的位置;(2)连接AE,根据直径的性质得出∠AEC=∠AEB=90°,根据AB=AC得出∠BAE=∠CAE,从而得出∠CAE=∠BAE,得出弧相等;(3)根据Rt△ACE的三角形函数得出CE的长度,根据(2)得出BE=CE=DE=4,根据Rt△BCD中∠B的三角函数得出BC和BD的长度,从而得出三角形周长.
试题解析:(1)如图1,⊙O为所求.
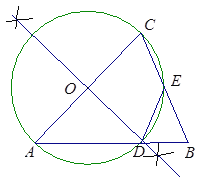
(2)证明:如图,连接AE, ∵AC为⊙O的直径,点E在⊙O上,∴∠AEC=90°,
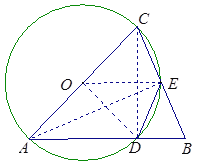
∵AB=AC,∴∠BAE =∠CAE, ∴![]() .
.
(3)解:如图在Rt△ACE中,
![]() ,
, ![]() ,∴
,∴![]() .
.
∵AB= AC,∠AEC=90°,∴∠B =∠ACB,BE= CE=4. 又![]()
![]() ,∴DE= CE=4.
,∴DE= CE=4.
在Rt△BCD中, ![]() , ∵
, ∵![]() ,BC=8,
,BC=8,
∴![]() ,
,
∴![]() 的周长
的周长![]()
![]() .
.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
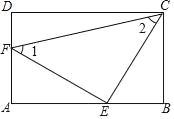
【题目】如图:在矩形ABCD中,E、F分别是AB、AD边上的点,且BE=AF,∠1=∠2.
(1)Rt△AEF与Rt△BCE全等吗?说明理由;
(2)△CEF是不是直角三角形?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
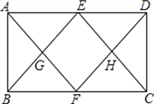
【题目】如图,在矩形ABCD中,E,F分别为AD,BC的中点,连结AF,DF,BE,CE,AF与BE交于G,DF与CE交于H.求证:四边形EGFH为菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一座钢结构桥梁的框架是△ABC,水平横梁BC长18米,中柱AD高6米,其中D是BC的中点,且AD⊥BC.
(1)求sinB的值;
(2)现需要加装支架DE、EF,其中点E在AB上,BE=2AE,且EF⊥BC,垂足为点F,求支架DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂原计划生产24000台空气净化器,由于雾霾天气的影响,空气净化器的需求量呈上升趋势,生产任务的数量增加了12000台.工厂在实际生产中,提高了生产效率,每天比原计划多生产100台,实际完成生产任务的天数是原计划天数的1.2倍.求原计划每天生产多少台空气净化器.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的一元二次方程:(m﹣1)x2+(m﹣2)x﹣1=0(m为实数).
(1)若方程有两个不相等的实数根,求m的取值范围;
(2)若![]() 是此方程的实数根,抛物线y=(m﹣1)x2+(m﹣2)x﹣1与x轴交于A、B,抛物线的顶点为C,求△ABC的面积.
是此方程的实数根,抛物线y=(m﹣1)x2+(m﹣2)x﹣1与x轴交于A、B,抛物线的顶点为C,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班在一次数学测验后成绩统计如下表:
分数段(分) | 40~49 | 50~59 | 60~69 | 70~79 | 80~89 | 90~100 |
人数 | 1 | 3 | 4 | 8 | 13 | 11 |
如果60分及以上为及格,那么这次数学测验的及格率是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的弦,半径OA=2,OA和AB的长度是关于x的一元二次方程x2﹣4x+a=0的两个实数根.
(1)求弦AB的长度;
(2)计算S△AOB;
(3)⊙O上一动点P从A点出发,沿逆时针方向运动一周,当S△POA=S△AOB时,求P点所经过的弧长(不考虑点P与点B重合的情形).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com