Question

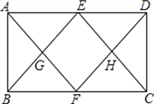
【题目】如图，在矩形ABCD中，E，F分别为AD，BC的中点，连结AF，DF，BE，CE，AF与BE交于G，DF与CE交于H．求证：四边形EGFH为菱形

Answer 1

【答案】证明见解析

【解析】试题分析: 根据一组对边平行且相等的四边形式平行四边形,可证明四边形AECF,BEDF是平行四边形,根据平行四边形的性质,可得GF与EH,EG与FH的关系,根据平行四边形的判定,可得EGFH的形状,根据三角形全等,可得EG与FG的关系,根据菱形的定义,可得证明结论．

试题解析:∵在矩形ABCD中AD=BC,且E,F分别是AD,BC的中点,

∴AE=DE=BF=CF,

又∵AD∥BC,

∴四边形AECF,BEDF是平行四边形,

∴GF∥EH,EG∥FH,

∴四边形EGFH是平行四边形,

在△AEG和△FBG中,,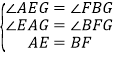

∴△AEG≌△FBG（AAS）,

∴EG=GB,AG=GF,

在△ABE和△BAF中,

∵

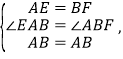
∴△ABE≌△BAF（SAS）,

∴AF=BE,

∵EG=GB=BE,AG=GF=AF,

∴EG=GF,

∴四边形EGFH是菱形.