
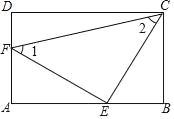
【题目】如图:在矩形ABCD中,E、F分别是AB、AD边上的点,且BE=AF,∠1=∠2.
(1)Rt△AEF与Rt△BCE全等吗?说明理由;
(2)△CEF是不是直角三角形?说明理由.
【答案】(1)结论:Rt△AEF与Rt△BCE全等(2)结论:△CEF是直角三角形.
【解析】试题分析:(1)根据HL,由BE=AF、EC=EF,即可证明;
(2)只要证明∠4+∠5=90°,即可解决问题;
试题解析:
(1)结论:Rt△AEF与Rt△BCE全等.
理由:在矩形ABCD中,∠A=∠B=90°
∵BE=AF,
∵∠1=∠2,
∴CE=EF
∴Rt△AEF≌Rt△BCE.
(2)结论:△CEF是直角三角形.
理由:∵Rt△AEF≌Rt△BCE.
∴∠3=∠5,
∵∠3+∠4=90°,∠5+∠4=90°,
∴∠CEF=180°﹣(∠4+∠5)=180°﹣90°=90°,
所以△CEF是直角三角形.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
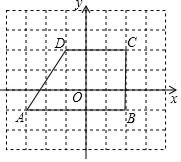
【题目】在直角坐标平面里,梯形ABCD各顶点的位置如图所示,图中每个小正方形方格的边长为1个单位长度.
(1)求梯形ABCD的面积;
(2)如果把梯形ABCD在坐标平面里先向右平移1个单位,然后向下平移2个单位得到梯形A1B1C1D1,求新顶点A1,B1,C1,D1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品的定价为每件20元,商场为了促销,决定如果购买5件以上,则超过5件的部分打7折.
(1)求购买这种商品的货款y (元)与购买数量x (件)之间的函数关系;
(2)当x=3,x=6时,货款分别为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E,F.

(1)求证:△ABE≌△CDF;
(2)若AC与BD交于点O,求证:AO=CO.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,二次函数y=ax2﹣5x+c的图象如图.
(1)求这个二次函数的解析式
(2)观察图象,回答:何时y随x的增大而增大;何时y随x的增大而减小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABC中,AB=AC=4![]() ,cosC=
,cosC=![]() .
.
(1)动手操作:利用尺规作以AC为直径的⊙O,并标出⊙O与AB的交点D,与BC的交点E(保留作图痕迹,不写作法).
(2)综合应用:在你所作的圆中,求证: ![]() ;
;
(3)求△BDE的周长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com