
 如图,在△ABC中,三角形内角平分线AD,BE,CF相交于点I,IH⊥BC于点H,求证:∠BID=∠HIC.
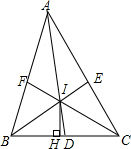
如图,在△ABC中,三角形内角平分线AD,BE,CF相交于点I,IH⊥BC于点H,求证:∠BID=∠HIC. 分析 根据角平分线的定义、三角形内角和定理可知∠BAD+∠ABI+∠HCI=90°.又因为∠BAD+∠ABI=∠BID,90°-∠HCI=∠CIH,所以∠BID=∠CIH.
解答 证明:∵AD,BE,CF为三角形ABC的角平分线,
∴∠BAD=$\frac{1}{2}$∠BAC,∠ABI=$\frac{1}{2}$∠ABC,∠HCI=$\frac{1}{2}$∠ACB.
∴∠BAD+∠ABI+∠HCI=$\frac{1}{2}$∠BAC+$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠ACB=$\frac{1}{2}$(∠BAC+∠ABC+∠ACB)=$\frac{1}{2}$×180°=90°.
∴∠BAD+∠ABI=90°-∠HCI.
又∵∠BAD+∠ABI=∠BID,90°-∠HCI=∠CIH
2(∠BAD+∠ABI+∠HCI)=180°,
∴∠BAD+∠ABI+∠HCI=90°,
∴∠BID=∠CIH.
点评 本题考查了角平分线的定义及三角形内角和定理,掌握三角形三个内角的和为180°是解决问题的关键.


 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
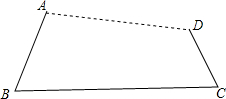 如图,用钉子把木棒AB、BC和CD分别在端点B、C处连接起来,用橡皮筋把AD连接起来
如图,用钉子把木棒AB、BC和CD分别在端点B、C处连接起来,用橡皮筋把AD连接起来查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在同一平面直角坐标系中画出函数y=$\frac{1}{2}$x2和y=2x2的图象
如图,在同一平面直角坐标系中画出函数y=$\frac{1}{2}$x2和y=2x2的图象查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com