
【题目】如图1,等腰直角![]() 中,
中,![]() ,
,![]() 过点
过点![]() ,
,![]() 的圆交
的圆交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连结
,连结![]() .
.
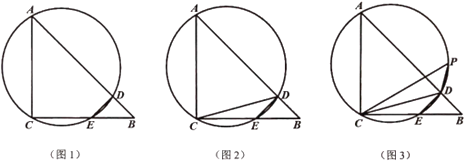
(1)若![]() ,
,![]() ,分别求
,分别求![]() ,
,![]() 的长
的长
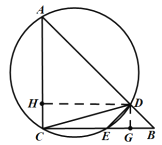
(2)如图2,连结![]() ,若
,若![]() ,
,![]() 的面积为10,求
的面积为10,求![]() .
.
(3)如图3,在圆上取点![]() 使得
使得![]() (点
(点![]() 与点
与点![]() 不重合),连结
不重合),连结![]() ,且点
,且点![]() 是
是![]() 的内心
的内心
①请你画出![]() ,说明画图过程并求
,说明画图过程并求![]() 的度数.
的度数.
②设![]() ,
,![]() ,
,![]() ,若
,若![]() ,求
,求![]() 的内切圆半径长.
的内切圆半径长.
【答案】(1)DE=![]() ;CE=
;CE=![]() ;(2)
;(2)![]() ;(3)①画图见解析;∠CDF=135°;②
;(3)①画图见解析;∠CDF=135°;②![]() 的内切圆半径为2.
的内切圆半径为2.
【解析】
(1)由A、C、E、D四点共圆可得∠ADE=90°,然后求出DE、BE、BC,再根据CE=BC-BE即可得出答案;
(2)过点D作DH⊥CA于H,过点D作DG⊥CB于G G,设DG=x,根据45°等腰直角三角形性质可得DG=EG=BG=x,根据△ACD面积列出关于x的式子求出x值,再据此计算tan∠BCD;
(3)①过点![]() 画
画![]() 交
交![]() 的延长线于点
的延长线于点![]() ,根据∠PFD=∠CFD,∠PCD=∠BCD,∠CPF=90°即可求出∠CDF的度数;②过点D作DG⊥CB于G,则DG为△CPF内切圆半径,先求出△CDE∽△DBF,根据相似三角形性质可得
,根据∠PFD=∠CFD,∠PCD=∠BCD,∠CPF=90°即可求出∠CDF的度数;②过点D作DG⊥CB于G,则DG为△CPF内切圆半径,先求出△CDE∽△DBF,根据相似三角形性质可得![]() ,然后求出BD=DE=
,然后求出BD=DE=![]() ,即可得出△CPF的内切圆半径长.
,即可得出△CPF的内切圆半径长.
解:(1)∵![]() ,
,![]() ,
,
∴![]() ,
,![]()

∵四边形![]() 内接于圆,
内接于圆,
∴![]()
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
(2)过点![]() 作
作![]() 于
于![]() ,过点
,过点![]() 作
作![]() 于
于![]()
![]() ,设
,设![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() ,
, ![]() ,
,
∵![]() 的面积为10,
的面积为10,
∴![]() ,
,
解得![]() ,
,![]() (舍去)
(舍去)
∴![]()
(3)①∵![]() ,点
,点![]() 为
为![]() 的内心,
的内心,
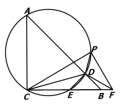
∴如图,过点![]() 画
画![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,
![]() 即为所求的三角形.
即为所求的三角形.
∵∠PFD=∠CFD,∠PCD=∠BCD,∠CPF=90°
∴![]()
=![]()
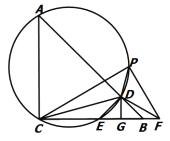
②过点![]() 作
作![]() 于
于![]() ,则
,则![]() 为
为![]() 内切圆半径
内切圆半径
∵![]() ,
,![]() ,
,
∴![]()
又∵![]() ,
,
∴![]()
而![]() ,
,
∴![]() .
.
∴![]() ,即
,即![]()
而![]()
∴![]() ,
,
∴![]() 的内切圆半径为2.
的内切圆半径为2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在趣味运动会“定点投篮”项目中,我校七年级八个班的投篮成绩![]() 单位:个
单位:个![]() 分别为:24,20,19,20,22,23,20,
分别为:24,20,19,20,22,23,20,![]() 则这组数据中的众数和中位数分别是
则这组数据中的众数和中位数分别是![]()
![]()
A. 22个、20个 B. 22个、21个 C. 20个、21个 D. 20个、22个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点P(x0,y0)到直线Ax+By+C=0(A2+B2≠0)的距离公式为:d=![]() ,
,
例如,求点P(1,3)到直线4x+3y﹣3=0的距离.
解:由直线4x+3y﹣3=0知:A=4,B=3,C=﹣3
所以P(1,3)到直线4x+3y﹣3=0的距离为:d=![]() =2
=2
根据以上材料,解决下列问题:
(1)求点P1(1,-1)到直线3x﹣4y﹣5=0的距离.
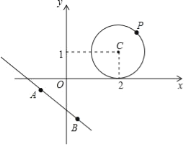
(2)已知:⊙C是以点C(2,1)为圆心,1为半径的圆,⊙C与直线y=﹣![]() x+b相切,求实数b的值;
x+b相切,求实数b的值;
(3)如图,设点P为问题2中⊙C上的任意一点,点A,B为直线3x+4y+5=0上的两点,且AB=2,请求出△ABP面积的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展“走进中国数学史”为主题的知识竞赛活动,八、九年级各有200名学生参加竞赛,为了解这两个年级参加竞赛学生的成绩情况,从中各随机抽取20名学生的成绩,数据如下:
八年级 | 91 | 89 | 77 | 86 | 71 | 九年级 | 84 | 93 | 66 | 69 | 76 |
51 | 97 | 93 | 72 | 91 | 87 | 77 | 82 | 85 | 88 | ||
81 | 92 | 85 | 85 | 95 | 90 | 88 | 67 | 88 | 91 | ||
88 | 88 | 90 | 64 | 91 | 96 | 68 | 97 | 99 | 88 |
整理上面数据,得到如下统计表:
成绩 人数 年级 |
|
|
|
|
|
八年级 | 1 | 1 | 3 | 7 | 8 |
九年级 | 0 | 4 | 2 | 8 | 6 |
样本数据的平均数、中位数、众数、方差如下表所示:
统计表 年级 | 平均数 | 中位数 | 众数 | 方差 |
八年级 | 83.85 | 88 | 91 | 127.03 |
九年级 | 83.95 | 87.5 | | 99.45 |
根据以上信息,回答下列问题:
(1)写出上表中众数![]() 的值.
的值.
(2)试估计八、九年级这次选拔成绩80分以上的人数和.
(3)你认为哪个年级学生的竞赛成绩较好?说明你的理由.(至少从两个不同的角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的港珠澳大桥是目前桥梁设计中广泛采用的斜拉桥,它用粗大的钢索将桥面拉住,为检测钢索的抗拉强度,桥梁建设方从甲、乙两家生产钢索的厂方各随机选取5根钢索进行抗拉强度的检测,数据统计如下(单位:百吨)

甲、乙两厂钢索抗拉强度检测统计表
钢索 | 1 | 2 | 3 | 4 | 5 | 平均数 | 中位数 | 方差 |
甲厂 | 10 | 11 | 9 | 10 | 12 | 10.4 | 10 | 1.04 |
乙厂 | 10 | 8 | 12 | 7 | 13 | a | b | c |
(1)求乙厂5根钢索抗拉强度的平均数a(百吨)、中位数b(百吨)和方差c(平方百吨).
(2)桥梁建设方决定从抗拉强度的总体水平和稳定性来决定钢索的质量,问哪一家的钢索质量更优?
查看答案和解析>>
科目:初中数学 来源: 题型:
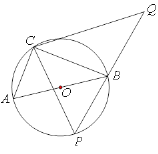
【题目】如图,在⊙O上有定点C和动点P,位于直径AB的异侧,过点C作CP的垂线,与PB的延长线交于点Q,已知:⊙O半径为![]() ,
,![]() ,则CQ的最大值是____________.
,则CQ的最大值是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图抛物线y=ax2+bx+c的对称轴为直线x=1,且过点(3,0),下列结论:①abc>0;②a﹣b+c<0;③2a+b>0;④b2﹣4ac>0;正确的有( )个.
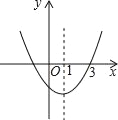
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
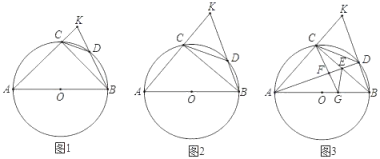
【题目】已知AB是⊙O的直径,点C是弧AB的中点,点D在弧BC上,BD、AC的延长线交于点K,连接CD.
(1)求证:∠AKB﹣∠BCD=45°;
(2)如图2,若DC=![]() DB时,求证:BC=2CK;
DB时,求证:BC=2CK;
(3)在(2)的条件下,连接BC交AD于点E,过点C作CF⊥AD于点F,延长CF交AB于点G,连接GE,若GE=5,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向的B处,求此时轮船所在的B处与灯塔P的距离.(参考数据:![]() ≈2.449,结果保留整数)
≈2.449,结果保留整数)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com