
【题目】(问题情境)
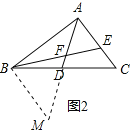
课外兴趣小组活动时,老师提出了如下问题:如图1,△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使DE=AD,连接BE.请根据小明的方法思考:
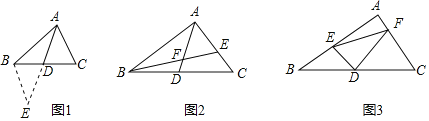
(1)由已知和作图能得到△ADC≌△EDB,依据是 .
A.SSS B.SAS C.AAS D.HL
(2)由“三角形的三边关系”可求得AD的取值范围是 .
解后反思:题目中出现“中点”“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.
(初步运用)
如图2,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.若EF=3,EC=2,求线段BF的长.
(灵活运用)
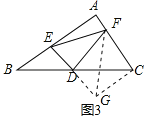
如图3,在△ABC中,∠A=90°,D为BC中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF,试猜想线段BE、CF、EF三者之间的等量关系,并证明你的结论.
【答案】(1)B;(2)2<AD<10;【初步运用】BF=5;【灵活运用】BE2+CF2=EF2,理由见解析
【解析】
(1)根据全等三角形的判定定理解答;
(2)根据三角形的三边关系计算;
初步运用 延长AD到M,使AD=DM,连接BM,证明△ADC≌△MDB,根据全等三角形的性质解答;
灵活运用 延长ED到点G,使DG=ED,连结GF,GC,证明△DBE≌△DCG,得到BE=CG,根据勾股定理解答.
解:(1)在△ADC和△EDB中,
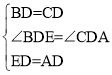 ,
,
∴△ADC≌△EDB(SAS),
故选:B;
(2)∵△ADC≌△EDB,
∴EB=AC=8,
在△ABE中,
AB﹣BE<AE<AB+BE,
∴2<AD<10,
故答案为:2<AD<10;
【初步运用】
延长AD到M,使AD=DM,连接BM,
∵AE=EF.EF=3,
∴AC=5,
∵AD是△ABC中线,
∴CD=BD,
∵在△ADC和△MDB中,
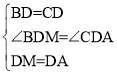 ,
,
∴△ADC≌△MDB,
∴BM=AC,∠CAD=∠M,
∵AE=EF,
∴∠CAD=∠AFE,
∵∠AFE=∠BFD,
∴∠BFD=∠CAD=∠M,
∴BF=BM=AC,
即BF=5;
【灵活运用】
线段BE、CF、EF之间的等量关系为:BE2+CF2=EF2.
证明:如图3,延长ED到点G,使DG=ED,连结GF,GC,
∵ED⊥DF,
∴EF=GF,
∵D是BC的中点,
∴BD=CD,
在△BDE和△CDG中,
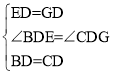 ,
,
∴△BDE≌△CDG(SAS),
∴BE=CG,
∵∠A=90°,
∴∠B+∠ACB=90°,
∵△BDE≌△CDG,EF=GF,
∴BE=CG,∠B=∠GCD,
∴∠GCD+∠ACB=90°,即∠GCF=90°,
∴Rt△CFG中,CF2+GC2=GF2,
∴BE2+CF2=EF2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )
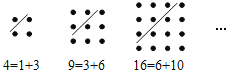
A.13=3+10B.25=9+16C.36=15+21D.49=18+31
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.
(1)该顾客至少可得到_____元购物券,至多可得到_______元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
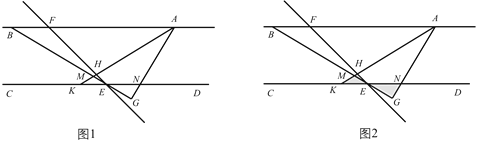
【题目】如图1,![]() ,点
,点![]() ,
,![]() 分别在直线
分别在直线![]() ,
,![]() 上,
上,![]() ,过点
,过点![]() 作
作![]() 的延长线交于点
的延长线交于点![]() ,交
,交![]() 于点
于点![]() ,
,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
(1)直接写出![]() ,
,![]() ,
,![]() 之间的关系:
之间的关系:
___________=____________+___________
(2)若![]() ,求
,求![]() .
.
(3)如图2,在(2)的条件下,将![]() 绕着点
绕着点![]() 以每秒
以每秒![]() 的速度逆时针旋转,旋转时间为
的速度逆时针旋转,旋转时间为![]() ,当
,当![]() 边与射线
边与射线![]() 重合时停止,则在旋转过程中,当
重合时停止,则在旋转过程中,当![]() 的其中一边与
的其中一边与![]() 的某一边平行时,直接写出此时
的某一边平行时,直接写出此时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
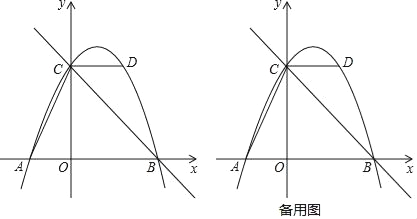
【题目】如图,抛物线y=ax2+bx+c的图象经过点A(﹣2,0),点B(4,0),点D(2,4),与y轴交于点C,作直线BC,连接AC、CD.
(1)求抛物线的函数表达式;
(2)E是抛物线上的点,求满足∠ECD=∠ACO的点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为准备母亲节礼物,同学们委托小明用其支付宝余额团购鲜花或礼盒.每束鲜花的售价相同,每份礼盒的售价也相同.若团购15束鲜花和18份礼盒,余额差80元;若团购18束鲜花和15份礼盒,余额剩70元.若团购19束鲜花和14份礼盒,则支付宝余额剩_______元.
查看答案和解析>>
科目:初中数学 来源: 题型:
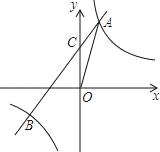
【题目】如图,反比例函数y=![]() 的图象与一次函数y=kx+b的图象交于点A(m,2),点B(﹣2,n ),一次函数图象与y轴的交点为C.
的图象与一次函数y=kx+b的图象交于点A(m,2),点B(﹣2,n ),一次函数图象与y轴的交点为C.
(1)求一次函数解析式;
(2)求C点的坐标;
(3)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线l经过点A,BD⊥直线l,CE⊥直线l,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线l上,且∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立;请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是直线l上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,求证:DF=EF.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com