
【题目】数学概念:百度百科上这样定义绝对值函数:y=│x│=![]()
并给出了函数的图像(如图).

方法迁移
借鉴研究正比例函数y=kx与一次函数y=kx+b(k,b是常数,且k≠0)之间关系的经验,我们来研究函数y=│x+a│(a是常数)的图像与性质.
“从‘1’开始”
我们尝试从特殊到一般,先研究当a=1时的函数y=│x+1│.
按照要求完成下列问题:
(1)观察该函数表达式,直接写出y的取值范围;
(2)通过列表、描点、画图,在平面直角坐标系中画出该函数的图像.
“从‘1’到一切”
(3)继续研究当a的值为-2,-![]() ,2,3,…时函数y=│x+a│的图像与性质,
,2,3,…时函数y=│x+a│的图像与性质,
尝试总结:
①函数y=│x+a│(a≠0)的图像怎样由函数y=│x│的图像平移得到?
②写出函数y=│x+a│的一条性质.
知识应用
(4)已知A(x1,y1),B(x2,y2)是函数y=│x+a│的图像上的任意两点,且满足x1<x2≤-1时, y1>y2,则a的取值范围是 .
【答案】(1)y≥0.(2)见解析;(3)①见解析;②答案不唯一,如当x>-a时,y随x的增大而增大;当x<-a时,y随x的增大而减小.(4)a≤1.
【解析】
(1)根据绝对值的概念可以写出答案;
(2)通过列表、描点、连线,即可画出函数图象;
(3)当a的值为-2和3时,通过列表、描点、连线,画出函数图象,通过观察图象得出①、②的答案;
(4)通过观察图象:函数y=│x+a│的对称轴为直线![]() ,根据函数的增减性,可以求得a的取值范围.
,根据函数的增减性,可以求得a的取值范围.
(1)根据绝对值的性质得: y≥0.
(2)列表:
x |
| -4 | -3 | -2 | -1 | 0 | 1 | 2 |
|
y=│x+1│ |
| 3 | 2 | 1 | 0 | 1 | 2 | 3 |
|
通过描点、连线,射线CA、CB就是所求作;

(3)当a的值为-2和3时,仿照(2)的方法在同一平面直角坐标系中画出函数的图像,如下图:
x |
| -1 | 2 | 5 |
|
y=│x-2│ |
| 3 | 0 | 3 |
|
x |
| -6 | -3 | 0 |
|
y=│x+3│ |
| 3 | 0 | 3 |
|

①函数y=│x+a│(a≠0)的图像是由函数y=│x│的图像向左(a>0)或向右(a<0)平移│a│个单位得到.
②答案不唯一,如:当x>-a时,y随x的增大而增大;当x<-a时,y随x的增大而减小.
(4)通过观察函数的图象知:函数y=│x+a│的对称轴为直线![]() ,
,
根据题意:满足x1<x2≤-1时, y1>y2,属于减函数,是在对称轴![]() 的左侧,
的左侧,
所以-1≤-a,
所以![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BD,CE分别是AC,AB边上的高,BD, CE交于O,则图中共有相似三角形( )

A. 5对 B. 6对 C. 7对 D. 8对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖同学学完统计知识后,随机调查了她所在辖区若干名居民的年龄,将调查数据绘制成如下扇形和条形统计图:

请根据以上不完整的统计图提供的信息,解答下列问题:
(1)小颖同学共调查了多少名居民的年龄,扇形统计图中a,b各等于多少?
(2)补全条形统计图;
(3)若该辖区年龄在0~14岁的居民约有1500人,请估计年龄在15~59岁的居民的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有个均匀的正十二面体的骰子,其中1个面标有“1”,2个面标有“2”,3个面标有“3”,2个面标有“4”,1个面标有“5”,其余面标有“6”,将这个骰子掷出后:
(1)掷出“6”朝上的可能性有多大?
(2)哪些数字朝上的可能性一样大?
(3)哪些数字朝上的可能性最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=1,AD=![]() ,BD=2,∠ABC+∠ADC=180°,CD=
,BD=2,∠ABC+∠ADC=180°,CD=![]() .
.
(1)判断△ABD的形状,并说明理由;
(2)求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
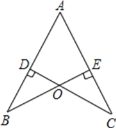
【题目】如图,已知AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
(1)问题探究:线段OB,OC有何数量关系,并说明理由;
(2)问题拓展:分别连接OA,BC,试判断直线OA,BC的位置关系,并说明理由;
(3)问题延伸:将题目条件中的“CD⊥AB于D,BE⊥AC于E”换成“D、E分别为AB,AC边上的中点”,(1)(2)中的结论还成立吗?请直接写出结论,不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,BE=EC,将正方形ABCD的边CD沿DE折叠到DF,连接EF、FC、FB,若△DFC的面积为16,则△BEF的面积为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com