练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

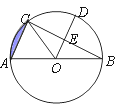
    【题目】如图，AB是⊙O的直径,BC是⊙O的弦，半径OD⊥BC,垂足为E，若BC=，OE=3；

    求：(1)⊙O的半径；

    (2)阴影部分的面积.

    【答案】（1）6；（2）.

    【解析】

    试题（1）利用垂径定理求得CE=,在Rt△COE中，由勾股定理求得CO的长度；

    （2）阴影部分的面积=扇形ACO的面积-△AOC的面积．

    试题解析：（1）∵BC是⊙O的弦，半径OD⊥BC，BC=，∴CE=BC=.

    ∴在Rt△COE中，由勾股定理得，,

    ∴⊙O的半径是6.

    （2）∵在Rt△COE中，∠CEO=90°，CO=2OE，∴∠ECO=30°．

    ∵AB是⊙O的直径，∴∠ACB=90°.∴∠ACO=60°．

    ∵OA=OC，∴△ACO是等边三角形.∴∠AOC=60°.

    ∴S阴影=S扇形ACO-S△AOC=.

    答：阴影部分的面积是．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

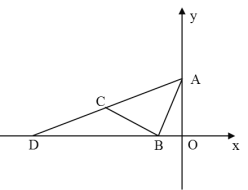
    【题目】如图，已知直线与轴、轴分别交于、两点，点，射线交轴的负半轴于点．

    （1）求点的坐标；

    （2）点是坐标平面内不同于点的一点，且以、、为顶点的三角形与全等，请直接写出点的坐标；

    （3）点是线段上一点，直线交于点，且的面积等于面积的一半，求点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=x2+2x与直线y= 交于A，B两点，与直线x=2交于点P，将抛物线沿着射线AB平移个单位．

    （1）平移后的抛物线顶点坐标为_______；

    （2）在整个平移过程中，点P经过的路程为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

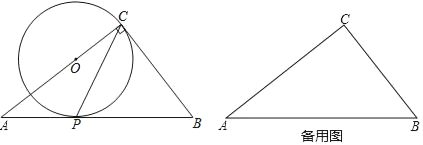
    【题目】如图，在△ABC中，∠ACB=90°，经过点C的⊙O与斜边AB相切于点P，AC=8，BC=6．

    （1）当点O在AC上时，求证：2∠ACP=∠B；

    （2）在（1）的条件下，求⊙O的半径．

    （3）若圆心O在△ABC之外，则CP的变化范围是　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠C=90°，AE平分∠BAC交BC于E，点O在AB上，以OA为半径的圆，交AB于D，交AC于C，且点E在⊙O上，连接DE，BF切⊙O于点F．

    (1)求证：BE=BF；

    (2)若⊙O的半径为R，AG=R+1，CE=R﹣1，求弦AG的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

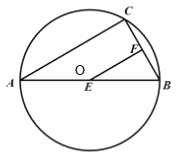
    【题目】如图，AB是⊙O的直径，弦BC=4cm，点F是弦BC的中点，∠ABC=60°，若动点E以2cm/s的速度在线段AB上由A向B运动，连接EF，设运动时间为t(s)，当△BEF是直角三角形时，t的值等于______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，BD、CE是△ABC的高.

    （1）试说明B、C、D、E四点在同一个圆上；

    （2）若S△ADE∶S△ABC=1∶4，BC=8，求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

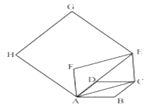
    【题目】如图，边长为1的菱形中，，连结对角线，以为边做第二个菱形，．连结，再以为边做第三个菱形，使…按此规律所作的第2015个菱形的边长是__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小冬与小夏是某中学篮球队的队员，在最近五场球赛中的得分如下表所示：

    第一场

    第二场

    第三场

    第四场

    第五场

    小冬

    小夏

    （1）根据上表所给的数据，填写下表：

    平均数

    中位数

    众数

    方差

    小冬

    小夏

    （2）根据以上信息，若教练选择小冬参加下一场比赛，教练的理由是什么？

    （3）若小冬的下一场球赛得分是分，则在小冬得分的四个统计量中（平均数、中位数、众数与方差）哪些发生了改变，改变后是变大还是变小？（只要回答是“变大”或“变小”）（）

    查看答案和解析>>

    同步练习册答案