
【题目】如图,在△ABC中,∠C=90°,AE平分∠BAC交BC于E,点O在AB上,以OA为半径的圆,交AB于D,交AC于C,且点E在⊙O上,连接DE,BF切⊙O于点F.
(1)求证:BE=BF;
(2)若⊙O的半径为R,AG=R+1,CE=R﹣1,求弦AG的长.

【答案】(1)证明见解析;(2)AG=6.
【解析】
(1)连接OE,证出OE⊥CD,再由切线长定理易得BE=BF;
(2)根据直径所对的圆周角得出∠AGD=90°,从而证得GD∥BC,进而证得OE⊥GD,根据垂径定理得出GH=DH,然后证得四边形GCEH是矩形,从而证得GD=2(R-1)=2R-2,最后根据勾股定理求得R,即可求得AG的长.
(1)连接DG、OE,交于点H.
∵AE平分∠BAC交BC于E,
∴∠CAE=∠DAE,
∵OA=OE,
∴∠OAE=∠OEA,
∴∠CAE=∠OEA,
∴AC∥OE,
∴∠OEB=∠C=90°,
∴OE⊥BC,
∴BC是圆的切线,
∴BE=BF;
(2)∵AB是直径,
∵∠AGD=90°,
∵∠C=90°,
∴GD∥BC,
∵OE⊥BC,
∴OE⊥GD,
∴GH=DH,
∵∠AGD=90°,∠C=90°,OE⊥BC,
∴四边形GCEH是矩形,
∴GH=CE=R﹣1,
∴GD=2(R﹣1)=2R﹣2,
在直角三角形AGD中,AG2+GD2=AD2 ,
即(R+1)2+(2R﹣2)2=(2R)2
解得R1=5,R2=1(舍去),
∴AG=R+1=5+1=6;


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】某宾馆拥有客房100间,经营中发现:每天入住的客房数y(间)与房价x(元)(180≤x≤300)满足一次函数关系,部分对应值如下表:
x(元) | 180 | 260 | 280 | 300 |
y(间) | 100 | 60 | 50 | 40 |
(1)求y与x之间的函数表达式;
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每间空置的客房,宾馆每日需支出各种费用60元.当房价为多少元时,宾馆当日利润最大?求出最大利润.(宾馆当日利润=当日房费收入-当日支出)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某型号新能源纯电动汽车充满电后,蓄电池剩余电量![]() (千瓦时)关于已行驶路程
(千瓦时)关于已行驶路程![]() (千米)的函数图象.
(千米)的函数图象.

(1)根据图象,直接写出蓄电池剩余电量为35千瓦时时汽车已行驶的路程,当![]() 时,求1千瓦时的电量汽车能行驶的路程;
时,求1千瓦时的电量汽车能行驶的路程;
(2)当![]() 时求
时求![]() 关于
关于![]() 的函数表达式,并计算当汽车已行驶180千米时,蓄电池的剩余电量.
的函数表达式,并计算当汽车已行驶180千米时,蓄电池的剩余电量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一边长为4正方形![]() 放在平面直角坐标系中,其中
放在平面直角坐标系中,其中![]() 为原点,点
为原点,点![]() 、
、![]() 分别在
分别在![]() 轴、
轴、![]() 轴上,
轴上,![]() 为射线
为射线![]() 上任意一点
上任意一点
(1)如图1,若点![]() 坐标为
坐标为![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,则
,则![]() 的面积为__________;
的面积为__________;
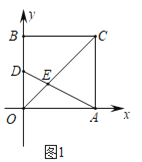
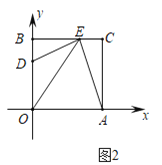
(2)如图2,将![]() 沿
沿![]() 翻折得
翻折得![]() ,若点
,若点![]() 在直线
在直线![]() 图象上,求出
图象上,求出![]() 点坐标;
点坐标;
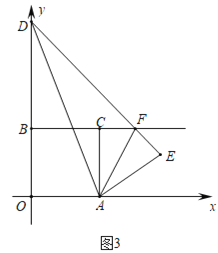
(3)如图3,将![]() 沿
沿![]() 翻折得
翻折得![]() ,
,![]() 和射线
和射线![]() 交于点
交于点![]() ,连接
,连接![]() ,若
,若![]() ,平面内是否存在点
,平面内是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为直角边的等腰直角三角形,若存在,请求出所有点
为直角边的等腰直角三角形,若存在,请求出所有点![]() 坐标:若不存在,请说明理由.
坐标:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
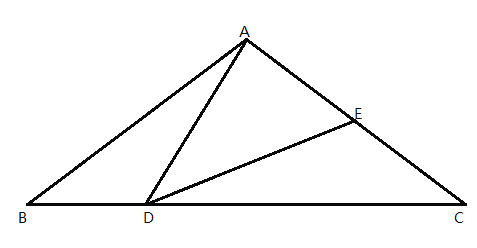
【题目】如图,![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上运动(点
上运动(点![]() 不与
不与![]() 、
、![]() 重合),连接
重合),连接![]() ,作
,作![]() ,
,![]() 交线段
交线段![]() 于
于![]()
(1)当![]() 时,
时,![]() ;
;
(2)当![]() 等于多少度时,
等于多少度时,![]() ≌
≌![]() ?请说明理由;
?请说明理由;
(3)![]() 能成为等腰三角形吗?若能,请直接写出
能成为等腰三角形吗?若能,请直接写出![]() 的度数;若不能,请说明理由
的度数;若不能,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,左右两幅图案关于y轴对称,右图案中的左右眼睛的坐标分别是(2,3),(4,3),嘴角左右端点的坐标分别是(2,1),(4,1).
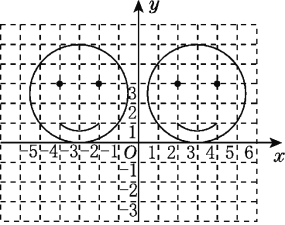
(1)试确定左图案中的左右眼睛和嘴角左右端点的坐标;
(2)从对称的角度来考虑,说一说你是怎样得到的;
(3)直接写出右图案中的嘴角左右端点关于原点的对称点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com