
【题目】如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E
(1)求证:DE=AB;
(2)以A为圆心,AB长为半径作圆弧交AF于点G,若BF=FC=1,求扇形ABG的面积.(结果保留π)

【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)根据矩形的性质得出∠B=90°,AD=BC,AD∥BC,求出∠DAE=∠AFB,∠AED=90°=∠B,根据AAS推出△ABF≌△DEA即可;
(2)根据勾股定理求出AB,解直角三角形求出∠BAF,根据全等三角形的性质得出DE=DG=AB=![]() ,∠GDE=∠BAF=30°,根据扇形的面积公式求得求出即可.
,∠GDE=∠BAF=30°,根据扇形的面积公式求得求出即可.
试题解析:(1)∵四边形ABCD是矩形,∴∠B=90°,AD=BC,AD∥BC,∴∠DAE=∠AFB,∵DE⊥AF,∴∠AED=90°=∠B,在△ABF和△DEA中,∵∠AFB=∠DAE,∠B=∠DEA,AF=AD,∴△ABF≌△DEA(AAS),∴DE=AB;
(2)∵BC=AD,AD=AF,∴BC=AF,∵BF=1,∠ABF=90°,∴由勾股定理得:AB=![]() =
=![]() ,∴∠BAF=30°,∵△ABF≌△DEA,∴∠GDE=∠BAF=30°,DE=AB=DG=
,∴∠BAF=30°,∵△ABF≌△DEA,∴∠GDE=∠BAF=30°,DE=AB=DG=![]() ,∴扇形ABG的面积=
,∴扇形ABG的面积=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣(x+h)2,当x<﹣3时,y随x的增大而增大,当x>﹣3时,y随x的增大而减小,当x=0时,y的值为( )
A. ﹣1B. ﹣9C. 1D. 9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( )
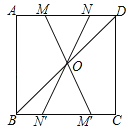
A.2对 B.3对 C.4对 D.5对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF.连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.
(1)请判断:FG与CE的数量关系是 ,位置关系是 ;
(2)如图2,若点E,F分别是边CB,BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请作出判断并给予证明;
(3)如图3,若点E,F分别是边BC,AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.
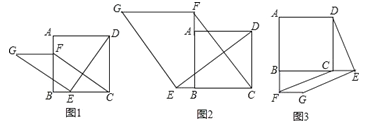
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图a是一个长为2m,宽为2n的长方形,沿图a中虚线用剪刀把它均分成四块小长方形,然后按图b的形状拼成一个正方形.
(1)请用两种不同的方法求图b中阴影部分的面积:
方法1: ____ (只列式,不化简)
方法2: ______ (只列式,不化简)
(2)观察图b,写出代数式(m+n)2,(m-n)2,mn之间的等量关系: ______ ;
(3)根据(2)题中的等量关系,解决如下问题:若a+b=7,ab=5,
则(a-b)2= ______ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次数学测试后,某班40名学生的成绩被分为5组,第1~4组的频数分别为12、10、6、8,则第5组的频率是( )
A.0.1
B.0.2
C.0.3
D.0.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数图象经过A(-4,-9)和B(3, 5)两点,与x轴的交于点C,与y轴的交于点D,
(1)求该一次函数解析式;
(2)点C坐标为___________ ,点D坐标为___________ ;
(3)求该一次函数图象和坐标轴围成的图形面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com