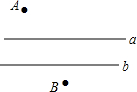练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．如图，幸福小区A和超市B位于公路的两侧，现要在公路上建一座天桥，天桥建在何处可使小区A的人到超市B购物最近？（假定公路的两边是平行的直线，天桥与公路垂直）

    分析 将点A竖直向下平移到点A′，使AA′等于公路的宽度，连接A′B，与b交于点Q，过点Q作PQ⊥a于P，连接AP、BQ．则由A经过天桥走到B的最短路线的长：AP+PQ+QB=A′B+PQ．

    解答 解：如图；①将点A竖直向下平移到点A′，使AA′等于公路的宽度，
    ②连接A′B，与b交于点Q，
    ③过点Q作PQ⊥a于P，
    ④连接AP、BQ．
    则天桥建在PQ处能使由A经过天桥走到B的路程最短，最短路线的长：AP+PQ+QB=A′B+PQ．

    点评 本题考查的是作图-应用与设计作图，涉及到轴对称-最短路线问题，平行四边形的判定与性质，根据“两点之间，线段最短”找到桥址的位置是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    8．按要求完成下列各小题．
    （1）计算：-|+$\frac{3}{8}$|+|-$\frac{7}{8}$|-|-$\frac{1}{2}$|
    （2）计算：$\frac{3}{2}-\frac{4}{5}+（-\frac{3}{5}）-（-\frac{7}{2}）$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

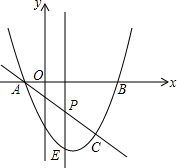    6．如图，抛物线y=x2-2x-3与x轴交A，B两点（A点在B点左侧），直线l与抛物线交于A，C两点，其中C点的横坐标为2．
    （1）求A，B 两点的坐标及直线AC的函数表达式；
    （2）P是线段AC上的一个动点，过P作y轴的平行线交抛物线于E点，求线段PE长度的最大值；
    （3）点G抛物线上的动点，在x轴上是否存在点F，使A，C，F，G这样的四个点为顶点的四边形是平行四边形？如果存在，求出所有满足条件的F点坐标；如果不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

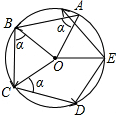    3．如图，小明从一个圆形场地边沿点A出发，按逆时针方向运动，先沿∠OAB=α的方向走到场地边沿的点B，再沿∠OBC=α的方向走到场地边沿的点C…，照此继续行走并依字母顺序标记，结果点F首次越过了点A并恰好处于$\widehat{AB}$的中点．如果小明希望下一次行走路线正好是⊙O的内接正九边形，那么他应将最初的角α增大或减小多少度？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

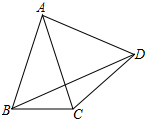    10．如图，△ABC中，AB=AC，∠BAC=40°，边AB绕点A逆时针旋转m°，（0＜m＜360）得到线段AD，连接BD、DC．若△BDC为等腰三角形，则m所有可能的取值是20°，80°，200°，320°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图，已知B，D为AE上的两点，BC，DF交于点G，∠A=∠2，CF∥AE，∠3=∠4．求证：∠1=∠E．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．已知|3a+6|+（1-b）2=0，求2a2-4ab+b2与-3a2+2ab-5b2的差．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．小明发现一个被墨水污染的数轴，根据图示写出被墨迹盖住部分的整数共有4个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．我们知道$\sqrt{2}$≈1.414，于是我们说：“$\sqrt{2}$的整数部分为1，小数部分则可记为$\sqrt{2}$-1”．则：
    （1）$\sqrt{2}$-3的整数部分为-1，小数部分则可记为$\sqrt{2}$-2；
    （2）已知3+$\sqrt{31}$的小数部分为a，7-$\sqrt{31}$的小数部分为b，那么a+b的值是1；
    （3）已知x是$\sqrt{10}$的整数部分，y是$\sqrt{10}$的小数部分，求${（y-\sqrt{10}）^{x-1}}$的平方根．

    查看答案和解析>>

    同步练习册答案