
【题目】如图是一张长10 dm,宽6 dm矩形纸板,将纸板四个角各剪去一个同样的边长为x dm的正方形,然后将四周突出部分折起,可制成一个无盖方盒.
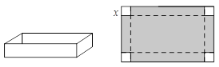
(1) 无盖方盒盒底的长为______dm,宽为_____dm(用含x的式子表示)
(2) 若要制作一个底面积是32dm2的一个无盖长方体纸盒,求剪去的正方形边长x.
科目:初中数学 来源: 题型:
【题目】如图 1,在平面直角坐标系中,点 O 是坐标原点,四边形 ABCO 是菱形,点 A 的坐标为(-3,4),点 C 在 x 轴的正半轴上,直线 AC 交 y 轴于点 M,AB 边交 y 轴于点 H.
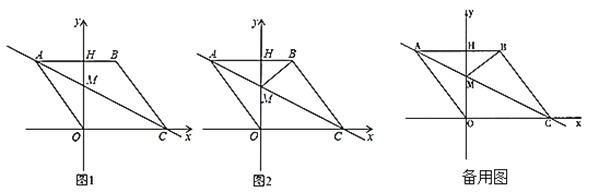
(1)求直线 AC 的解析式;
(2)连接 BM,如图 2,动点 P 从点 A 出发,沿折线 ABC 方向以 2 个单位/秒的速度向终点 C 匀速运动,设△PMB 的面积为 S(S≠0),点 P 的运动时间为 t 秒,求 S 与 t 之间的函数关系式(要求写出自变量 t 的取值范围);
(3)在(2)的条件下,当 t 为何值时,∠MPB 与∠BCO 互为余角,并求此时直线 OP 与直线 AC 所夹锐角的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
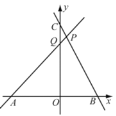
【题目】如图,在平面直角坐标系xOy中,已知直线PA是一次函数![]() 的图象,直线PB是一次函数
的图象,直线PB是一次函数![]() 的图象,点P是两直线的交点,点A、B、C、Q分别是两条直线与坐标轴的交点.若四边形PQOB的面积是5.5,且
的图象,点P是两直线的交点,点A、B、C、Q分别是两条直线与坐标轴的交点.若四边形PQOB的面积是5.5,且![]() ,若存在一点D,使以A、B、P、D为顶点的四边形是平行四边形,则点D的坐标为________.
,若存在一点D,使以A、B、P、D为顶点的四边形是平行四边形,则点D的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线![]() 与x轴、y轴分别交于点A、B,抛物线
与x轴、y轴分别交于点A、B,抛物线![]() 经过点A,将点B向右平移5个单位长度,得到点C,若抛物线与线段BC恰有一个公共点,则
经过点A,将点B向右平移5个单位长度,得到点C,若抛物线与线段BC恰有一个公共点,则![]() 的取值范围是____.
的取值范围是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
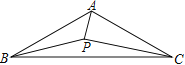
【题目】如图,△ABC中,AB=AC,点P为△ABC内一点,∠APB=∠BAC=120°.若AP+BP=4,则PC的最小值为( )
A. 2B. ![]() C.
C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李明准备进行如下操作实验,把一根长40 cm的铁丝剪成两段,并把每段首尾相连各围成一个正方形.
(1)要使这两个正方形的面积之和等于58 cm2,李明应该怎么剪这根铁丝?
(2)李明认为这两个正方形的面积之和不可能等于48 cm2,你认为他的说法正确吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
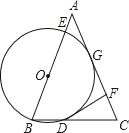
【题目】如图,AB=AC,点O在AB上,⊙O过点B,分别与BC、AB交于D、E,过D作DF⊥AC于F.
(1)求证:DF是⊙O的切线;
(2)若AC与⊙O相切于点G,⊙O的半径为3,CF=1,求AC长.
查看答案和解析>>
科目:初中数学 来源: 题型:
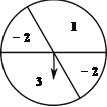
【题目】如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止)
(1)转动转盘一次,求转出的数字是-2的概率;
(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=16cm,BC=6cm,动点P、Q分别以3cm/s、2cm/s的速度从点A、C同时出发,点Q从点C向点D移动.
(1)若点P从点A移动到点B停止,点Q随点P的停止而停止移动,点P、Q分别从点A、C同时出发,问经过多长时间P、Q两点之间的距离是10cm?
(2)若点P沿着AB→BC→CD移动,点P、Q分别从点A、C同时出发,点Q从点C移动到点D停止时,点P随点Q的停止而停止移动,试探求经过多长时间△PBQ的面积为12cm2?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com