
【题目】直线![]() 与x轴、y轴分别交于点A、B,抛物线
与x轴、y轴分别交于点A、B,抛物线![]() 经过点A,将点B向右平移5个单位长度,得到点C,若抛物线与线段BC恰有一个公共点,则
经过点A,将点B向右平移5个单位长度,得到点C,若抛物线与线段BC恰有一个公共点,则![]() 的取值范围是____.
的取值范围是____.
【答案】![]() 或
或![]() 或
或![]() .
.
【解析】
根据坐标轴上点的坐标特征可求点A,B的坐标,根据平移的性质可求点C的坐标,结合图形,分三种情况:①a>0;②a<0,③抛物线的顶点在线段BC上;进行讨论即可求解.
解:与x轴交点:令y=0代入直线y=4x+4得x=-1,
∴A(-1,0),
与y轴交点:令x=0代入直线y=4x+4得y=4,
∴B(0,4),
∵点B向右平移5个单位长度,得到点C,
∴C(5,4)
将点A(-1,0)代入抛物线![]() 中得
中得![]() ,即
,即![]()
∴抛物线的对称轴![]()
由抛物线的对称性可知抛物线也一定过A的对称点(3,0),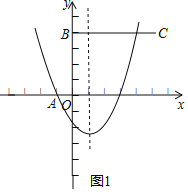
①a>0时,如图1,将x=0代入抛物线得![]() ,
,
∵抛物线与线段BC恰有一个公共点,
∴![]() ,
,
∴![]()
将![]() 代入抛物线得
代入抛物线得![]() ,
,
∴![]() ,
,
∴![]() ;
;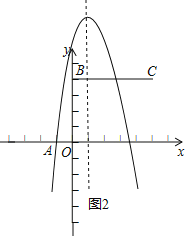
②a<0时,如图2,
将x=0代入抛物线得![]() ,
,
∵抛物线与线段BC恰有一个公共点,
∴![]() ,
,
∴![]() ;
;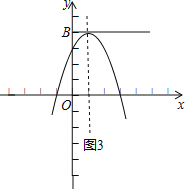
③当抛物线的顶点在线段BC上时,则顶点为(1,4),如图3,
将点(1,4)代入抛物线得,
解得![]() .
.
综上所述,![]() 或
或![]() 或
或![]() .
.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】已知点P在一次函数y=kx+b(k,b为常数,且k<0,b>0)的图象上,将点P向左平移1个单位,再向上平移2个单位得到点Q,点Q也在该函数y=kx+b的图象上.
(1)k的值是 ;
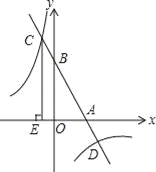
(2)如图,该一次函数的图象分别与x轴、y轴交于A,B两点,且与反比例函数y=![]() 图象交于C,D两点(点C在第二象限内),过点C作CE⊥x轴于点E,记S1为四边形CEOB的面积,S2为△OAB的面积,若
图象交于C,D两点(点C在第二象限内),过点C作CE⊥x轴于点E,记S1为四边形CEOB的面积,S2为△OAB的面积,若![]() =
=![]() ,则b的值是 .
,则b的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作第1个正方形A1B1C1C;延长C1B1交x轴于点A2,作第2个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
解方程x4–7x2+12=0,这是一个一元四次方程,根据该方程的特点,它的解法通常是:
设x2=y,则x4=y2.
∴原方程可化为y2–7y+12=0.
∴a=1,b=–7,c=12.
∴△=b2–4ac=(–7)2–4×1×12=1.
∴y═![]() =–
=–![]() .
.
解得y1=3,y2=4.
当y=3时,x2=3,x=±![]() .
.
当y=4时,x2=4,x=±2.
∴原方程有四个根是:x1=![]() ,x2=–
,x2=–![]() ,x3=2,x4=–2.
,x3=2,x4=–2.
以上方法叫换元法,达到了降次的目的,体现了数学的转化思想,运用上述方法解答下列问题.
(1)解方程:(x2+x)2–5(x2+x)+4=0;
(2)已知实数a,b满足(a2+b2)2–3(a2+b2)–10=0,试求a2+b2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
问题:已知方程x2+x﹣1=0,求一个一元二次方程,使它的根分别是已知方程根的2倍.
解:设所求方程的根为y,则y=2x,所以x=![]() ,把x=
,把x=![]() ,代入已知方程,
,代入已知方程,
得(![]() )2 +
)2 +![]() ﹣1=0.
﹣1=0.
化简,得y2+2y﹣4=0,
故所求方程为y2+2y﹣4=0
这种利用方程根的代换求新方程的方法,我们称为“换根法”.
请用阅读材料提供的“换根法”求新方程(要求:把所求方程化为一般形式):
(1)已知方程x2+2x﹣1=0,求一个一元二次方程,使它的根分别是已知方程根的相反数,则所求方程为 ;
(2)已知关于x的一元二次方程ax2+bx+c=0(a≠0)有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程根的倒数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一张长10 dm,宽6 dm矩形纸板,将纸板四个角各剪去一个同样的边长为x dm的正方形,然后将四周突出部分折起,可制成一个无盖方盒.
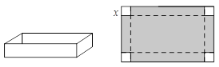
(1) 无盖方盒盒底的长为______dm,宽为_____dm(用含x的式子表示)
(2) 若要制作一个底面积是32dm2的一个无盖长方体纸盒,求剪去的正方形边长x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,点P为AC边上的一点,延长BP至点D,使得AD=AP,当AD⊥AB时,过D作DE⊥AC于E,AB-BC=4,AC=8,则△ABP面积为_____
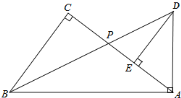
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com