
【题目】如图 1,在平面直角坐标系中,点 O 是坐标原点,四边形 ABCO 是菱形,点 A 的坐标为(-3,4),点 C 在 x 轴的正半轴上,直线 AC 交 y 轴于点 M,AB 边交 y 轴于点 H.
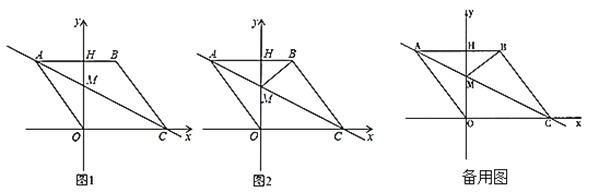
(1)求直线 AC 的解析式;
(2)连接 BM,如图 2,动点 P 从点 A 出发,沿折线 ABC 方向以 2 个单位/秒的速度向终点 C 匀速运动,设△PMB 的面积为 S(S≠0),点 P 的运动时间为 t 秒,求 S 与 t 之间的函数关系式(要求写出自变量 t 的取值范围);
(3)在(2)的条件下,当 t 为何值时,∠MPB 与∠BCO 互为余角,并求此时直线 OP 与直线 AC 所夹锐角的正切值.
【答案】(1)![]() ;(2)
;(2)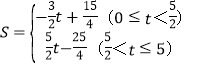 ;(3)当t=
;(3)当t=![]() 时,∠MPB与∠BCO互为余角,直线OP与直线AC所夹锐角的正切值为
时,∠MPB与∠BCO互为余角,直线OP与直线AC所夹锐角的正切值为![]() ;当t=
;当t=![]() 时,∠MPB与∠BCO互为余角,直线OP与直线AC所夹锐角的正切值为1.
时,∠MPB与∠BCO互为余角,直线OP与直线AC所夹锐角的正切值为1.
【解析】
(1)已知A点的坐标,就可以求出OA的长,根据OA=OC,就可以得到C点的坐标,根据待定系数法就可以求出函数解析式;
(2)点P的位置应分P在AB和BC上两种情况进行讨论:当P在AB上时,S=![]() BPMH;当P在BC上时,S=
BPMH;当P在BC上时,S=![]() P1BBM,据此面积就可以表示出来;
P1BBM,据此面积就可以表示出来;
(3)分两种情况进行讨论,当P点在AB边上运动时:设OP与AC相交于点Q连接OB交AC于点K,证明△AQP∽△CQO,根据相似三角形的对应边的比相等,以及勾股定理可以求出AQ,QC的长,在直角△OHB中,根据勾股定理,可以得到tan∠OQC.当P点在BC边上运动时,可证△BHM∽△PBM和△PQC∽△OQA,根据相似三角形的对应边的比相等,就可以求出OK,KQ就可以求出.
解:(1)过点A作AE⊥x轴垂足为E,如图(1),
∵A(3,4),
∴AE=4 ,OE=3,
∴OA=![]() =5,
=5,
∵四边形ABCO为菱形,
∴OC=OA=5,
∴C(5,0)
设直线AC的解析式为:y=kx+b(k≠0),
∴![]() ,解得:
,解得: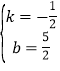 ,
,
∴直线AC的解析式为:![]() ;
;
(2)由(1)得M点坐标为(0,![]() ),
),
∴OM=![]() ,
,
如图(1),当P点在AB边上运动时,
由题意得OH=4,
∴HM=OHOM=4![]() =
=![]() ,
,
∴S=BPMH=
![]() (52t)·
(52t)·![]() =
=![]() t+
t+![]() (0≤t<
(0≤t<![]() ),
),
当P点在BC边上运动时,记为P1,
∵∠OCM=∠BCM,CO=CB,CM=CM,
∴△OMC≌△BMC,
∴OM=BM=![]() ,∠MOC=∠MBC=90°,
,∠MOC=∠MBC=90°,
∴S=![]() P1BBM=
P1BBM=![]() (2t5)·
(2t5)·![]() =
=![]() t
t![]() (
(![]() <t≤5),
<t≤5),
综上所述: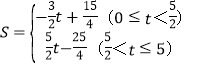 ;
;
(3)设OP与AC相交于点Q连接OB交AC于点K,
∵∠AOC=∠ABC,
∴∠AOM=∠ABM,
∵∠MPB+∠BCO=90°,∠BAO=∠BCO,∠BAO+∠AOH=90°,
∴∠MPB=∠AOH,
∴∠MPB=∠MBH.
当P点在AB边上运动时,如图(2),
∵∠MPB=∠MBH,
∴PM=BM,
∵MH⊥PB,
∴PH=HB=2,
∴PA=AHPH=1,
∴t=![]() ,
,
∵AB∥OC,
∴∠PAQ=∠OCQ,
∵∠AQP=∠CQO,
∴△AQP∽△CQO,
∴![]() ,
,
在Rt△AEC中,AC=![]() ,
,
∴AQ=![]() ,QC=
,QC=![]() ,
,
在Rt△OHB中,OB=![]() ,
,
∵AC⊥OB,OK=KB,AK=CK,
∴OK=![]() ,AK=KC=
,AK=KC=![]() ,
,
∴QK=AKAQ=![]() ,
,
∴tan∠OQC=![]() ;
;
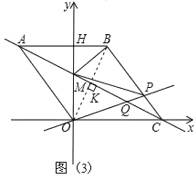
当P点在BC边上运动时,如图(3),
∵∠BHM=∠PBM=90°,∠MPB=∠MBH,
∴tan∠MPB=tan∠MBH,
∴![]() ,即
,即![]() ,
,
∴BP=![]() ,
,
∴t=![]() ,
,
∴PC=BCBP=5![]() =
=![]() .
.
由PC∥OA,同理可证△PQC∽△OQA,
∴![]() ,
,
∴CQ=![]() AC=
AC=![]() ,
,
∴QK=KCCQ=![]() ,
,
∵OK=![]() ,
,
∴tan∠OQK=![]() ,
,
综上所述,当t=![]() 时,∠MPB与∠BCO互为余角,直线OP与直线AC所夹锐角的正切值为
时,∠MPB与∠BCO互为余角,直线OP与直线AC所夹锐角的正切值为![]() ;当t=
;当t=![]() 时,∠MPB与∠BCO互为余角,直线OP与直线AC所夹锐角的正切值为1.
时,∠MPB与∠BCO互为余角,直线OP与直线AC所夹锐角的正切值为1.
img src="http://thumb.zyjl.cn/questionBank/Upload/2020/11/27/07/a1be0c08/SYS202011270738489031565345_DA/SYS202011270738489031565345_DA.030.png" width="199" height="189" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />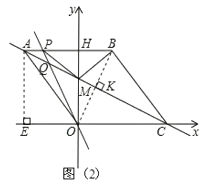


科目:初中数学 来源: 题型:
【题目】如图,已知直线l1:y=2x+1、直线l2:y=﹣x+7,直线l1、l2分别交x轴于B、C两点,l1、l2相交于点A.
(1)求A、B、C三点坐标;
(2)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
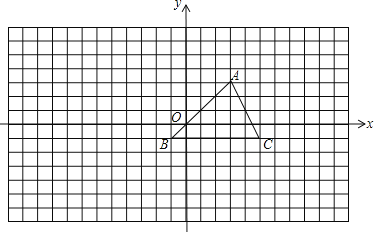
【题目】如图,方格中的每个小方格都是边长为1的正方形,我们把以格点间的连线为边的三角形称为“格点三角形”,图中的△ABC是格点三角形.在建立平面直角坐标系后,点B的坐标为(-1,-1).
(1)把△ABC向左平移8格后得到△A1B1C1,画出△A1B1C1的图形并写出点B1的坐标;
(2)把△ABC绕点C按顺时针旋转90°后得△A2B2C2,画出△A2B2C2的图形并写出B2的坐标;
(3)把△ABC以点A为位似中心放大,使放大前后对应边的比为1∶2,画出△AB3C3的图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
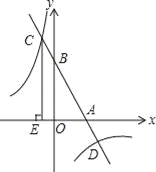
【题目】已知点P在一次函数y=kx+b(k,b为常数,且k<0,b>0)的图象上,将点P向左平移1个单位,再向上平移2个单位得到点Q,点Q也在该函数y=kx+b的图象上.
(1)k的值是 ;
(2)如图,该一次函数的图象分别与x轴、y轴交于A,B两点,且与反比例函数y=![]() 图象交于C,D两点(点C在第二象限内),过点C作CE⊥x轴于点E,记S1为四边形CEOB的面积,S2为△OAB的面积,若
图象交于C,D两点(点C在第二象限内),过点C作CE⊥x轴于点E,记S1为四边形CEOB的面积,S2为△OAB的面积,若![]() =
=![]() ,则b的值是 .
,则b的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,对角线AC,BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( ).
A. AB∥DC,AD∥BCB. AB=DC,AD=BC
C. AO=CO,BO=DOD. AB∥DC,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小刚用如图所示的两个转盘做配紫色游戏,游戏规则是:分别旋转两个转盘,若其中一个转盘转出了红色,另一个转出了蓝色,则可以配成紫色.此时小刚获胜,否则小明获胜.
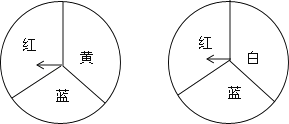
(1)利用画树状图或列表法表示游戏所有可能出现的结果.
(2)这个游戏对双方公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作第1个正方形A1B1C1C;延长C1B1交x轴于点A2,作第2个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一张长10 dm,宽6 dm矩形纸板,将纸板四个角各剪去一个同样的边长为x dm的正方形,然后将四周突出部分折起,可制成一个无盖方盒.
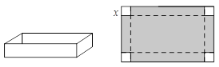
(1) 无盖方盒盒底的长为______dm,宽为_____dm(用含x的式子表示)
(2) 若要制作一个底面积是32dm2的一个无盖长方体纸盒,求剪去的正方形边长x.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com