
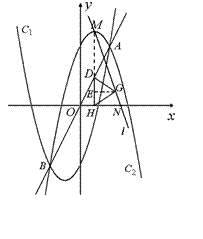
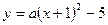 , C2:
, C2: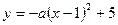 ,C1与C2的交点为A,
,C1与C2的交点为A,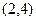 ,点B的横坐标是-2.
,点B的横坐标是-2.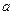 的值及点B的坐标;
的值及点B的坐标; 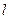 ,且
,且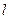 与x轴交于点N.
与x轴交于点N.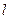 过△DHG的顶点G,点D的坐标为(1, 2),求点N的横坐标;
过△DHG的顶点G,点D的坐标为(1, 2),求点N的横坐标;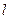 与△DHG的边DG相交,求点N的横坐标的取值范围.
与△DHG的边DG相交,求点N的横坐标的取值范围.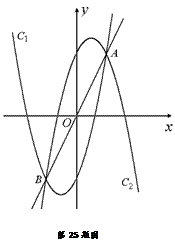
 )∵点A
)∵点A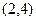 在抛物线C1上,
在抛物线C1上,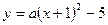 得
得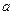 ="1" ……………………………………(2分)
="1" ……………………………………(2分)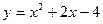
 ,
, , EH=1,
, EH=1,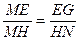 ,
,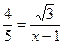 , ∴
, ∴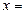
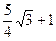 …………(5分))
…………(5分))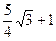 .
.  移到与点A重合时,如图2,
移到与点A重合时,如图2,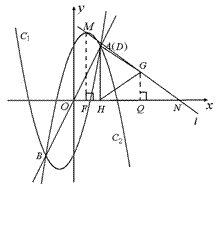
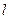 与
与 DG交于点G,此时点N的横坐标最大.
DG交于点G,此时点N的横坐标最大. (x,0)
(x,0)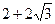 , 2)
, 2)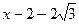 NF =
NF =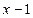 GQ="2 " MF =5.
GQ="2 " MF =5.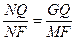
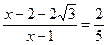
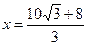 . ………………………………………………………(7分)
. ………………………………………………………(7分) 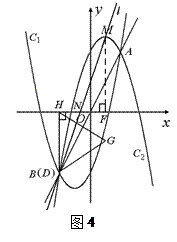
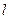 与DG交于点D,即点B
与DG交于点D,即点B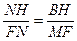
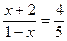 ∴
∴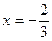

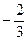 ≤x≤
≤x≤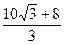 ………………………………(8分)
………………………………(8分)

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源:不详 题型:解答题
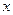 轴相交于点F,点Q为直线AD上一点,且△ABQ与△ADF相似,直接写出点Q点的坐标.
轴相交于点F,点Q为直线AD上一点,且△ABQ与△ADF相似,直接写出点Q点的坐标.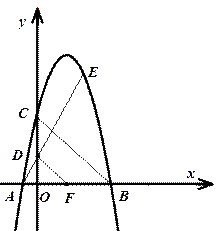
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
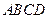 中,
中,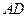 ∥
∥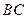 ,且
,且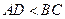 ,
, ,
,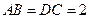 。
。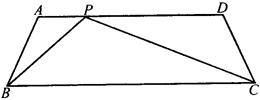
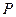 为
为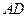 上的一点,满足
上的一点,满足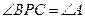 ,求
,求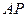 的长;
的长;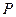 在
在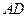 边上移动(点
边上移动(点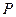 与点
与点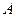 、
、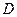 不重合),且满足
不重合),且满足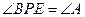 ,
,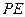 交直线
交直线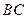 于点
于点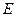 ,同时交直线
,同时交直线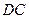 于点
于点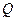 。
。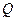 在线段
在线段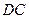 的延长线上时,设
的延长线上时,设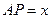 ,
,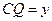 ,求
,求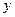 关于
关于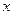 的函数关系式,并写出自变量
的函数关系式,并写出自变量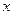 的取值范围;
的取值范围;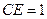 时,写出
时,写出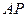 的长(不必写解答过程)
的长(不必写解答过程)查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 灯罩底
灯罩底 面半径MK的长;
面半径MK的长;
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
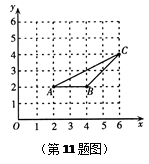
| A.(3,2) | B.(-3,-2)或(3,2) |
C.(2,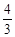 ) ) | D.(2,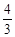 )或(-2,- )或(-2,-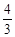 ) ) |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 (k>0)的图象过点E与直线l1相交于点F.
(k>0)的图象过点E与直线l1相交于点F.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com