
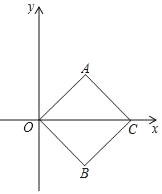
【题目】如图,四边形AOBC是正方形,点C的坐标是(4![]() ,0).
,0).
(Ⅰ)正方形AOBC的边长为 ,点A的坐标是 .
(Ⅱ)将正方形AOBC绕点O顺时针旋转45°,点A,B,C旋转后的对应点为A′,B′,C′,求点A′的坐标及旋转后的正方形与原正方形的重叠部分的面积;
(Ⅲ)动点P从点O出发,沿折线OACB方向以1个单位/秒的速度匀速运动,同时,另一动点Q从点O出发,沿折线OBCA方向以2个单位/秒的速度匀速运动,运动时间为t秒,当它们相遇时同时停止运动,当△OPQ为等腰三角形时,求出t的值(直接写出结果即可).
【答案】(1)4,![]() ;(2)旋转后的正方形与原正方形的重叠部分的面积为
;(2)旋转后的正方形与原正方形的重叠部分的面积为![]() ;(3)
;(3)![]() .
.
【解析】
(1)连接AB,根据△OCA为等腰三角形可得AD=OD的长,从而得出点A的坐标,则得出正方形AOBC的面积;
(2)根据旋转的性质可得OA′的长,从而得出A′C,A′E,再求出面积即可;
(3)根据P、Q点在不同的线段上运动情况,可分为三种列式①当点P、Q分别在OA、OB时,②当点P在OA上,点Q在BC上时,③当点P、Q在AC上时,可方程得出t.
解:(1)连接AB,与OC交于点D,
四边形![]() 是正方形,
是正方形,
∴△OCA为等腰Rt△,
∴AD=OD=![]() OC=2
OC=2![]() ,
,
∴点A的坐标为![]() .
.
4,![]() .
.
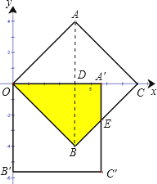
(2)如图
∵ 四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() .
.
∵ 将正方形![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,
,
∴ 点![]() 落在
落在![]() 轴上.
轴上.
∴![]() .
.
∴ 点![]() 的坐标为
的坐标为![]() .
.
∵![]() ,
,
∴![]() .
.
∵ 四边形![]() ,
,![]() 是正方形,
是正方形,
∴![]() ,
,![]() .
.
∴![]() ,
,![]() .
.
∴![]() .
.
∴![]() .
.
∵![]() ,
,
![]() ,
,
∴![]()
![]() .
.
∴旋转后的正方形与原正方形的重叠部分的面积为![]() .
.
(3)设t秒后两点相遇,3t=16,∴t=![]()
①当点P、Q分别在OA、OB时,
∵![]() ,OP=t,OQ=2t
,OP=t,OQ=2t
∴![]() 不能为等腰三角形
不能为等腰三角形
②当点P在OA上,点Q在BC上时如图2,

当OQ=QP,QM为OP的垂直平分线,
OP=2OM=2BQ,OP=t,BQ=2t-4,
t=2(2t-4),
解得:t=![]() .
.
③当点P、Q在AC上时,
![]() 不能为等腰三角形
不能为等腰三角形
综上所述,当![]() 时
时![]() 是等腰三角形
是等腰三角形


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案科目:初中数学 来源: 题型:
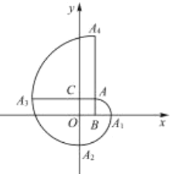
【题目】如图,在平面直角坐标系中,四边形![]() 是正方形,点
是正方形,点![]() 的坐标为
的坐标为![]() ,弧
,弧![]() 是以点
是以点![]() 为圆心,
为圆心,![]() 为半径的圆弧;弧
为半径的圆弧;弧![]() 是以点
是以点![]() 为圆心,
为圆心,![]() 为半径的圆弧,弧
为半径的圆弧,弧![]() 是以点
是以点![]() 为圆心,
为圆心,![]() 为半径的圆弧,弧
为半径的圆弧,弧![]() 是以点
是以点![]() 为圆心,
为圆心,![]() 为半径的圆弧.继续以点
为半径的圆弧.继续以点![]() ,
,![]() ,
,![]() ,
,![]() 为圆心按上述作法得到的曲线
为圆心按上述作法得到的曲线![]() …称为正方形的“渐开线”,则点
…称为正方形的“渐开线”,则点![]() 的坐标是__________.
的坐标是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
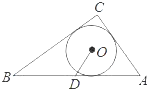
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,⊙O为△ABC的内切圆,点D是斜边AB的中点,则tan∠ODA=( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级举行英语演讲比赛,准备用1200元钱(全部用完)购买A,B两种笔记本作为奖品,已知A,B两种每本分别为12元和20元,设购入A种x本,B种y本.
(1)求y关于x的函数表达式.
(2)若购进A种的数量不少于B种的数量.
①求至少购进A种多少本?
②根据①的购买,发现B种太多,在费用不变的情况下把一部分B种调换成另一种C,调换后C种的数量多于B种的数量,已知C种每本8元,则调换后C种至少有______本(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以边上AC上一点O为圆心,OA为半径作⊙O,⊙O恰好经过边BC的中点D,并与边AC相交于另一点F.

(1)求证:BD是⊙O的切线.
(2)若AB=![]() ,E是半圆
,E是半圆![]() 上一动点,连接AE,AD,DE.
上一动点,连接AE,AD,DE.
填空:
①当![]() 的长度是____________时,四边形ABDE是菱形;
的长度是____________时,四边形ABDE是菱形;
②当![]() 的长度是____________时,△ADE是直角三角形.
的长度是____________时,△ADE是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以边上AC上一点O为圆心,OA为半径作⊙O,⊙O恰好经过边BC的中点D,并与边AC相交于另一点F.
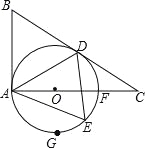
(1)求证:BD是⊙O的切线.
(2)若AB=![]() ,E是半圆
,E是半圆![]() 上一动点,连接AE,AD,DE.
上一动点,连接AE,AD,DE.
填空:
①当![]() 的长度是____________时,四边形ABDE是菱形;
的长度是____________时,四边形ABDE是菱形;
②当![]() 的长度是____________时,△ADE是直角三角形.
的长度是____________时,△ADE是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线![]() ,经过点A(-1,-2),B(0,1).
,经过点A(-1,-2),B(0,1).
(1)求抛物线的关系式及顶点P的坐标.
(2)若点B′与点B关于x轴对称,把(1)中的抛物线向左平移m个单位,平移后的抛物线经过点B′,设此时抛物线顶点为点P′.
①求∠P′B B′的大小.
②把线段P′B′以点B′为旋转中心顺时针旋转120°,点P′落在点M处,设点N在(1)中的抛物线上,当△MN B′的面积等于6![]() 时,求点N的坐标.
时,求点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() :
:![]() 与直线
与直线![]() :
:![]() 交于点
交于点![]() ,则
,则![]() ______.
______.

【答案】-1
【解析】
将点A的坐标代入两直线解析式得出关于m和b的方程组,解之可得.
解:由题意知![]() ,
,
解得![]() ,
,
故答案为:![]() .
.
【点睛】
本题主要考查两直线相交或平行问题,解题的关键是掌握两直线的交点坐标必定同时满足两个直线解析式.
【题型】填空题
【结束】
11
【题目】如图,长方形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则△AFC的面积等于___.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com